练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．先化简，再求值：（$\frac{2}{a+1}$+$\frac{a+2}{{a}^{2}-1}$）÷$\frac{a}{a+1}$，其中a=（-1）2016+tan60°．

    分析 先把括号内的通分计算，再把除法转换为乘法计算化简，最后代值计算．

    解答 解：（1）原式=$\frac{2（a-1）+（a+2）}{（a+1）（a-1）}$×$\frac{a+1}{a}$=$\frac{3a}{（a-1）（a+1）}$•$\frac{a+1}{a}$=$\frac{3}{a-1}$
    当a=（-1）2016+tan60°=1+$\sqrt{3}$时，
    原式=$\frac{3}{1+\sqrt{3}-1}$=$\sqrt{3}$．

    点评 此题考查分式的化简求值、特殊角的三角函数值等知识点，难度中等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

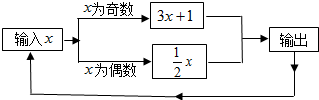    7．有一个数值转换器，原理如图所示，若开始输入的值是5，可发现第1次输出的结果是16，第2次输出的结果是8，依次继续下去…，第101次输出的结果是（　　）
    A．1B．16C．4D．8

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．某玩具厂生产一种玩具，据市场调查，若按每个玩具280元销售时，每月可销售300个，若销售单价每降低1元，每月可多售出2个，据统计，每个玩具的固定成本Q（元）与月销量y（个）满足如下关系：
    月销量y（个）…160200240300…
    每个玩具的固定成本Q（元）…60484032…
    （1）写出月销量y（个）与销售单价x（元）之间的函数关系式；
    （2）求每个玩具的固定成本Q（元）与月销量y（个）之间的函数关系式；
    （3）若每个玩具的固定成本为30元，则它占销售单价的比例是多少？（用分数表示）
    （4）若该厂这种玩具的月销量不超过400个，则每个玩具的固定成本至少为多少元？销售单价最低为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．现有甲、乙两个不透明的口袋，其中甲袋中装有三个小球，乙袋中装有两个小球，每个小球上都标有一个数字，甲袋中小球上数字分别为1，-2，3，乙袋中小球上数字分别为4，-5，每个小球除数字不同外其余均相同，小晶先从甲口袋中随机摸出一个小球，记下数字；再从乙口袋中随机摸出一个小球记下数字．请用画树状图（或列表）的方法，求小晶两次摸出的小球数字之积是负数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，已知BD是矩形ABCD的对角线．
    （1）作线段BD的垂直平分线，分别交AD、BC于点E、F（用尺规作图法，保留作图痕迹，不要求写作法）；
    （2）在（1）的条件下，连接BE、DF，问四边形BEDF是什么特殊四边形？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列数中比$\sqrt{5}$大的是（　　）
    A．-3B．0C．4D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．（1）计算：${（-\frac{1}{3}）}^{-1}$-$\sqrt{9}$+$（\sqrt{2}+1）^{0}$-2cos45°
    （2）化简：（a2-a）÷$\frac{{a}^{2}-2a+1}{a-1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

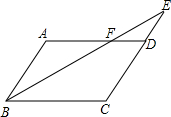    6．如图，?ABCD中，E是CD的延长线上一点，BE与AD交于点F，且AF=2FD．
    （1）求证：△ABF∽△CEB；
    （2）若△CEB的面积为9，求?ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．①解不等式组$\left\{\begin{array}{l}{2-x＞0}\\{\frac{5x+1}{2}+1≥\frac{2x-1}{3}}\end{array}\right.$
    ②计算：-12+|$\sqrt{3}-2$|+$（\frac{1}{2}）^{-1}$-5×（2009-π）0．

    查看答案和解析>>

    同步练习册答案