

 CF;
CF; 绕点B顺时针方向旋转
绕点B顺时针方向旋转 (00<
(00< <3600),如图②,是否存在某位置,使得
<3600),如图②,是否存在某位置,使得 ?,若存在,求出所有可能的旋转角
?,若存在,求出所有可能的旋转角 的大小;若不存在,请说明理由;
的大小;若不存在,请说明理由; (00<
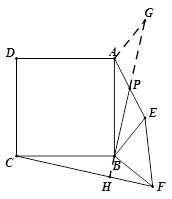
(00< <900),如图③,取AE的中点P,连接BP、CF,求证:BP=
<900),如图③,取AE的中点P,连接BP、CF,求证:BP= CF且BP⊥CF.
CF且BP⊥CF.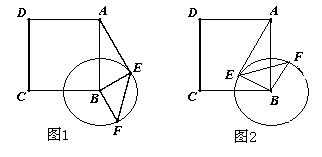
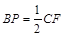
 绕点B顺时针方向旋转一周,E、F分别在以点B为圆心,BE为半径的圆周上,如图1,因此过A点做圆B的切线,设切点是点E,此时
绕点B顺时针方向旋转一周,E、F分别在以点B为圆心,BE为半径的圆周上,如图1,因此过A点做圆B的切线,设切点是点E,此时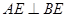 ,有AE∥BF。
,有AE∥BF。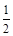 AB∴∠BAE = 30°
AB∴∠BAE = 30°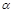 是60°…………(6分)
是60°…………(6分)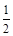 AB ∴∠BAE = 30°
AB ∴∠BAE = 30°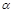 是300°
是300°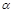 ∴∠ABE =
∴∠ABE = 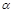 ,∠CBF = 180°-
,∠CBF = 180°-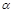
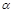
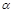 ∴∠GAB = ∠CBF
∴∠GAB = ∠CBF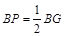 ∴
∴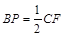 …………(11分)
…………(11分)

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源:不详 题型:解答题
 平面直角坐标系中,已知,ΔABO的三个顶点的坐标分别为A(2,2),B(0,4),O(0,0);
平面直角坐标系中,已知,ΔABO的三个顶点的坐标分别为A(2,2),B(0,4),O(0,0);  0并写出点A
0并写出点A ,B
,B 的坐标;
的坐标;
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com