
����Ŀ����ͼ��������y��ax2+bx+3��x�ύ��A(1��0)��B(��3��0)���㣬��y�ύ�ڵ�C���������ߵĶ���ΪD��
(1)��������ߵĽ���ʽ�붥��D�����꣮
(2)���жϡ�BCD����״����˵�����ɣ�
(3)����E��x���ϣ���Q���������ϣ��Ƿ������B��C��E��QΪ��������BCΪһ�ߵ�ƽ���ı��Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
(4)̽�����������Ƿ���ڵ�P��ʹ����P��A��CΪ��������������BCD���ƣ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
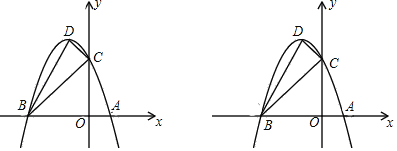
���𰸡�(1) �����ߵĽ���ʽΪy����x2��2x+3������D������Ϊ(��1��4)��(2) ��BCD��ֱ�������Σ����ɼ�������(3) Q�������Ϊ(��2��3)��(![]() ��1����3)��(��
��1����3)��(��![]() ��1����3)�� (4) ���������ĵ�P������Ϊ��(0��0)��(0����
��1����3)�� (4) ���������ĵ�P������Ϊ��(0��0)��(0����![]() )��(��9��0)��
)��(��9��0)��
��������
��1�����ô���ϵ����������ú����Ľ���ʽ��
��2�����ù��ɶ��������BCD�����ߵij���Ȼ����ݹ��ɶ������涨�����������жϣ�
��3����B��C��E��QΪ������ı�����ƽ���ı��Σ�������������ٵ�Q���������Ϊ3ʱ���ڵ���Q�������ꩁ3ʱ���������ʽ������ã�
��4����P��x���y������������ۣ����P�����꣬�������������εĶ�Ӧ�ߵı���ȼ�����⣮
(1)������y��ax2+bx+3��x�ύ��A(1��0)��B(��3��0)���㣬
��![]() ��
��
���a����1��b����2��
�������ߵĽ���ʽΪy����x2��2x+3��
��y����x2��2x+3����(x+1)2+4��
�ඥ��D������Ϊ(��1��4)��
(2)��BCD��ֱ�������Σ�
�������£���ͼ1������D�ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪE��F��

����Rt��BOC��OB��3��OC��3��
��BC2��OB2+OC2��18��
��Rt��CDF��DF��1��CF��OF��OC��4��3��1��
��CD2��DF2+CF2��2��
��Rt��BDE��DE��4��BE��OB��OE��3��1��2��
��BD2��DE2+BE2��20��
��BC2+CD2��BD2
���BCDΪֱ�������Σ�
(3)�ٵ�Q���������Ϊ3ʱ��
���y��3����y����x2��2x+3���x��0��2��
��Q1(��2��3)��
�ڵ�Q���������Ϊ��3ʱ��
��y����3����y����x2��2x+3���x��![]() ��1��
��1��![]() ��1��
��1��
��Q2(![]() ��1����3)��Q3(��
��1����3)��Q3(��![]() ��1����3)��
��1����3)��
���ϣ�Q�������Ϊ(��2��3)��(![]() ��1����3)��(��
��1����3)��(��![]() ��1����3)��
��1����3)��
(4)��(2)֪BC��3![]() ��CD��
��CD��![]() ��BD��2
��BD��2![]() ��
��
�١�![]() ��
��![]() ���ʵ�P��ԭ��Oʱ����ACP�ס�DBC��
���ʵ�P��ԭ��Oʱ����ACP�ס�DBC��
�ڵ�AC��ֱ�DZ�ʱ����AC��CD�Ƕ�Ӧ�ߣ�
��P��������(0��a)����PC��3��a��![]() ����
����![]() ��
��
��ã�a����9��
��P��������(0����9)��������ACP����ֱ�������Σ�����ACP�ס�CBD��������
�۵�AC��ֱ�DZߣ���AC��BC�Ƕ�Ӧ��ʱ��
��P��������(0��b)����PC��3��b����![]() ����
����![]() ��
��
��ã�b����![]() ��
��
��P��(0����![]() )ʱ������ACP�ס�CBDһ��������
)ʱ������ACP�ס�CBDһ��������
�ܵ�P��x����ʱ��AC��ֱ�DZߣ�Pһ����B����࣬��P��������(d��0)��
��AP��1��d����AC��CD�Ƕ�Ӧ��ʱ��![]() ����
����![]() ��
��
��ã�d��1��3![]() ����ʱ�����������β����ƣ�
����ʱ�����������β����ƣ�
�ݵ�P��x����ʱ��AC��ֱ�DZߣ�Pһ����B����࣬��P��������(e��0)��
��AP��1��e����AC��DC�Ƕ�Ӧ��ʱ��![]() ����
����![]() ��
��
��ã�e����9������������
���ϣ����������ĵ�P������Ϊ��(0��0)��(0����![]() )��(��9��0)��
)��(��9��0)��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2��bx��c��a��0���ĶԳ���Ϊx����1����x���һ������Ϊ(2��0)��������x��һԪ���η���ax2��bx��c��p��p��0��������������p��ֵ�У� ��
A. 2��B. 3��C. 4��D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
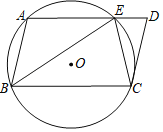
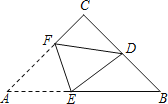
����Ŀ����ͼ����ABCD�У���A��B��C����ġ�O��AD�ڵ�E������BE��CE��BE��BC��
��1����֤����BEC�ס�CED��
��2����BC��10��DE��3.6�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
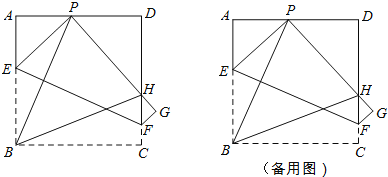
����Ŀ����ͼ��ʾ������һ�ű߳�Ϊ4��������ֽƬABCD����PΪ������AD���ϵ�һ�㣨�����A����D�غϣ���������ֽƬ�۵���ʹ��B����P������C����G����PG��DC��H���ۺ�ΪEF������BP��BH��
��1����֤����APB=��BPH��
��2������P�ڱ�AD���ƶ�ʱ����PDH���ܳ��Ƿ����仯����֤����Ľ��ۣ�
��3����APΪx���ı���EFGP�����ΪS�����S��x�ĺ�����ϵʽ������S�Ƿ������Сֵ�������ڣ���������Сֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��б��AC����һ�ô���AO��������̨���Ӱ�����б����ͼ��б��AC���½�Ϊ30�㣬AC��![]() �ף�����AO����б����60�㣬����AO�ij�Ϊ3�ף����ڵ�����B�����������O������Ϊ60�㣬���B��б���¶�C֮��ľ��룮
�ף�����AO����б����60�㣬����AO�ij�Ϊ3�ף����ڵ�����B�����������O������Ϊ60�㣬���B��б���¶�C֮��ľ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
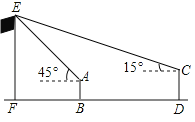
����Ŀ��ijУ�ţ�1���չ��ѧ����������Ż���λͬѧ�����ò���Dz���ѧУ��˵ĸ߶ȣ�����վ��B������˶���E�������Ϊ45�㣬�Ż�վ��D��D����ֱ��FB�ϣ������˶���E������Ϊ15�㣬��֪�������Ż���ࣨBD��30�ף����������ߣ�AB��1.6�ף��Ż������ߣ�CD��1.75�ף�����˵ĸ�EF�ij����������ȷ��0.1���ο����ݣ�sin15���0.26��cos15���0.97��tan15���0.27��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�CA��CB����C��90�㣬��D��BC���е㣬����ABC����ֱ��EF�۵���ʹ��A���D�غϣ��ۺ۽�AB�ڵ�E����AC�ڵ�F����ôsin��BED��ֵΪ��������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=6��BC=12����D�ڱ�BC�ϣ���E���߶�AD�ϣ�EF��AC�ڵ�F��EG��EF��AB�ڵ�G����EF=EG����CD�ij�Ϊ�� ��
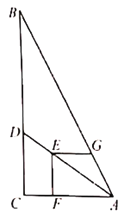
A.3.6B.4C.4.8D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BD��ABCD�ĶԽ��ߣ�AB��BD��BD=8cm��AD=10cm������P�ӵ�D��������5cm/s���ٶ���DA�˶����յ�A��ͬʱ����Q�ӵ�B������������BD-DC�˶����յ�C����BD��DC�Ϸֱ���8cm/s��6cm/s���ٶ��˶�������Q��QM��AB��������AB�ڵ�M������PQ����PQ��QMΪ������PQMN�����P���˶�ʱ��Ϊt��s����t��0����PQMN��ABCD�ص�����ͼ�ε����ΪS��cm2����

��1��AP= cm���ú�t�Ĵ���ʽ��ʾ����
��2������N���ڱ�AB��ʱ����t��ֵ��
��3����S��t֮��ĺ�����ϵʽ��
��4������NQ����NQ����ABD��һ��ƽ��ʱ��ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com