
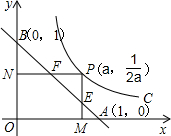
 如图,已知动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM丄x轴于点M,PN丄y轴于点N,线段PM、PN分别与直线AB:y=-x+1交于点E,F,求AF•BE的值.
如图,已知动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM丄x轴于点M,PN丄y轴于点N,线段PM、PN分别与直线AB:y=-x+1交于点E,F,求AF•BE的值. 分析 由点P(a,$\frac{1}{2a}$),求出点 F、E坐标,然后利用勾股定理用a表示AF,BE,即可求出AF•BE.
解答 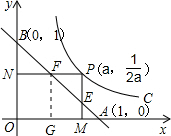 解:作FG⊥x轴,
解:作FG⊥x轴,
∵P的坐标为(a,$\frac{1}{2a}$),且PN⊥OB,PM⊥OA,
∴N的坐标为(0,$\frac{1}{2a}$),M点的坐标为(a,0),
∴BN=1-$\frac{1}{2a}$,
在直角三角形BNF中,∠NBF=45°(OB=OA=1,三角形OAB是等腰直角三角形),
∴NF=BN=1-$\frac{1}{2a}$,
∴F点的坐标为(1-$\frac{1}{2a}$,$\frac{1}{2a}$),
同理可得出E点的坐标为(a,1-a),
∴AF2=(1-1+$\frac{1}{2a}$)2+($\frac{1}{2a}$)2=$\frac{1}{2{a}^{2}}$,BE2=(a)2+(-a)2=2a2,
∴AF2•BE2=$\frac{1}{2{a}^{2}}$•2a2=1,即AF•BE=1.
点评 本题考查反比例函数的有关性质、一次函数的有关性质、勾股定理等知识,解题的关键是通过反比例函数上的点P来确定E、F两点的坐标,进而通过坐标系中两点的距离公式得出所求的值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | $2\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯,并设甲在a层出电梯,乙在b层出电梯.
小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯,并设甲在a层出电梯,乙在b层出电梯.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 上网时间 | 优惠标准 |
| 0~30小时(不超过30) | 无优惠 |
| 30~50小时(不超过50) | 通讯费优惠30% |
| 50~100小时(不超过100) | 通讯费优惠40% |
| 100小时以上 | 通讯费优惠50% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图.在图中,
如图.在图中,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com