
已知 ABCD的两边AB、AD的长是关于x的方程
ABCD的两边AB、AD的长是关于x的方程 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的边长为2,那么 ABCD的周长是多少?
ABCD的周长是多少?
(1)1, ;(2)5.
;(2)5.
【解析】
试题分析:(1)根据菱形四边相等的性质可知AB=AD,从而由一元二次方程有两个相等的实数根,根的判别式等于0即可求得;(2)由方程根满足方程的性质,可求出根是2时m的值,从而求出方程得另一根,然后根据平行四边形的性质求出周长.
试题解析:(1)∵ ABCD是菱形,∴AB=AD.
ABCD是菱形,∴AB=AD.
又∵ ,
,
当 ,即m=1时,四边形ABCD是菱形.
,即m=1时,四边形ABCD是菱形.
把m=1代入 ,得
,得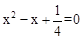 ,解得
,解得 .
.
∴菱形ABCD的边长是 .
.
(2)把AB=2代入 ,得
,得 ,
解得
,
解得 .
.
把 代入
代入 ,得
,得 . 解得
. 解得 ,
, . ∴AD=
. ∴AD= .
.
∵四边形ABCD是平行四边形,∴ ABCD的周长是2(2+
ABCD的周长是2(2+ )=5.
)=5.
考点:1.菱形的判定;2.方程根的性质;3.一元二次方程根的判别式;4.解一元二次方程;5.平行四边形的性质.


科目:初中数学 来源: 题型:
| 17 |
| 17 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:新课标3维同步训练与评价数学 九年级(下) 题型:044
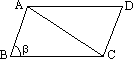
如图,在![]() ABCD中,AB=a,BC=b,∠ABC=β,试用a,b,β表示
ABCD中,AB=a,BC=b,∠ABC=β,试用a,b,β表示![]() ABCD的面积,如果已知△ABC的两边分别为a,b且夹角为α,你能否得出△ABC的面积呢?
ABCD的面积,如果已知△ABC的两边分别为a,b且夹角为α,你能否得出△ABC的面积呢?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com