
分析 (1)首先计算乘方和开方,然后从左向右依次计算即可.
(2)首先计算开方,然后从左向右依次计算即可.
(3)根据平方根的求法,求出x的值是多少即可.
(4)根据立方根的求法,求出x的值是多少即可.
解答 解:(1)(-1)2-|1-$\sqrt{2}$|+$\root{3}{27}$
=1-$\sqrt{2}$+1+3
=5-$\sqrt{2}$
(2)$\sqrt{3}$+$\sqrt{(-3)^{2}}$-$\root{3}{-8}$-|$\sqrt{3}$-2|
=$\sqrt{3}$+3-(-2)-2+$\sqrt{3}$
=3+2$\sqrt{3}$
(3)∵( x-1)2=4,
∴x-1=±2,
解得x=3或-1.
(4)3x3=-81
∴x3=-27,
∴x=-3.
点评 此题主要考查了实数的运算,以及立方根的求法,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
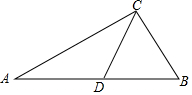 如图,在△ABC中,CD是边AB上的中线,∠B是锐角,且sinB=$\frac{\sqrt{2}}{2}$,tanA=$\frac{1}{2}$,AC=3$\sqrt{5}$
如图,在△ABC中,CD是边AB上的中线,∠B是锐角,且sinB=$\frac{\sqrt{2}}{2}$,tanA=$\frac{1}{2}$,AC=3$\sqrt{5}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
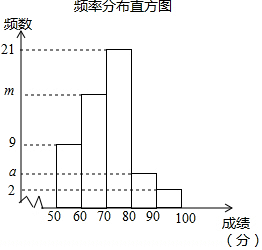 为参加学校的“我爱古诗词”知识竞赛,王晓所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.请根据以上频率分布表和频率分布直方图,回答下列问题:
为参加学校的“我爱古诗词”知识竞赛,王晓所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.请根据以上频率分布表和频率分布直方图,回答下列问题:| 组别 | 分组 | 频数 | 频率 |
| 1 | 50≤x<60 | 9 | 0.18 |
| 2 | 60≤x<70 | a | b |
| 3 | 70≤x<80 | 21 | 0.42 |
| 4 | 80≤x<90 | m | 0.06 |
| 5 | 90≤x≤100 | 2 | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com