
如图,已知一条直线过点 ,且与抛物线
,且与抛物线 交于
交于 两点,其中点
两点,其中点 的横坐标是
的横坐标是 .
.
⑴求这条直线的函数关系式及点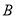 的坐标 ;
的坐标 ;
⑵在 轴上是否存在点
轴上是否存在点 ,使得△
,使得△ 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
⑶过线段 上一点
上一点 ,作
,作 ∥
∥ 轴,交抛物线于点
轴,交抛物线于点 ,点
,点 在第一象限;点
在第一象限;点 ,当点
,当点 的横坐标为何值时,
的横坐标为何值时, 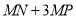 的长度最大?最大值是多少?
的长度最大?最大值是多少?

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源:江苏省扬州市邗江区2018届九年级上学期期末考试数学试卷 题型:解答题
解方程:
(1)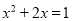 (2)
(2)
查看答案和解析>>
科目:初中数学 来源:北京市延庆区2017-2018学年第一学期八年级期末数学试卷 题型:单选题
如果把 中的
中的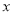 和
和 都扩大5倍,那么分式的值( )
都扩大5倍,那么分式的值( )
A. 扩大5倍 B. 不变 C. 缩小5倍 D. 扩大4倍
B 【解析】【解析】 分式中的x和y都扩大5倍,得=,那么这个分式的值不变,故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海口市八年级数学科期末检测模拟题(实验班卷) 题型:单选题
如图,E为正方形ABCD对角线AC上一点,若AE=BC,则∠BED等于( )
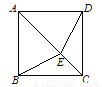
A. 115° B. 125° C. 135° D. 150°
C 【解析】∵四边形ABCD是正方形,AC是对角线, ∴AB=BC,∠BAE=45°, ∵AE=BC,∴AB=AE, ∴∠ABE=∠AED=(180°-45°)÷2 =67.5°, 同理可求得:∠AED=67.5°, ∴∠BED=2×67.5°=135°, 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海口市八年级数学科期末检测模拟题(实验班卷) 题型:单选题
若x2-x+M=(x-4)·N,则M、N分别为( )
A. -12,x+3 B. 20,x-5 C. 12,x-3 D. -20,x+5
A 【解析】∵(x-4)(x+3)=x2+3x-4x-12=x2-x-12, ∴M=-12,N=x+3, 故选A查看答案和解析>>
科目:初中数学 来源:四川省自贡市2017-2018学年上学期九年级期末统一考试数学试卷 题型:解答题
如图,点A的坐标为 ,点B的坐标为
,点B的坐标为 ,点C的坐标为
,点C的坐标为 .
.
⑴请在平面直角坐标系中画出?ABC向上平移2个单位后的图形?A1B1C1.
⑵请在直角坐标系中画出?ABC绕点C逆时针旋转90°的三角形为?A′B′C′,直接写出点A′的坐标 , 点B′的坐标
, 点B′的坐标 .
.

查看答案和解析>>
科目:初中数学 来源:四川省自贡市2017-2018学年上学期九年级期末统一考试数学试卷 题型:填空题
圆的内接四边形 ,已知
,已知 ,
, 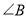 =__________ .
=__________ .
查看答案和解析>>
科目:初中数学 来源:浙江杭州淳安2016-2017学年七年级上学期期末数学试卷 题型:解答题
已知关于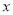 的方程
的方程 和
和 的解相同.
的解相同.
( )求
)求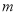 的值.
的值.
( )求式子
)求式子 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:广西柳州市2018届九年级上学期期末考试数学试卷 题型:单选题
如图,BC是⊙O的直径,点A是⊙O上异于B,C的一点,则∠A的度数为( )

A. 60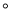 B. 70
B. 70 C. 80
C. 80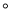 D. 90
D. 90
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com