
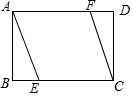
 如图,矩形ABCD中,AD=3,AB=2,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DF的长是( )
如图,矩形ABCD中,AD=3,AB=2,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DF的长是( )| A. | $\sqrt{5}$ | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{13}{6}$ |
分析 如图作EH⊥CF于H.首先证明四边形AECF是平行四边形,再证明△ABE≌△EHC,推出BE=CH,设DF=BE=x,在Rt△EHC中利用勾股定理即可解决问题.
解答 解:如图作EH⊥CF于H.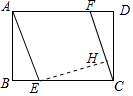
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∵AE∥CF,
∴四边形AECF是平行四边形,
∠AEB=∠ECH,
∴AF=CE,DF=BE,设DF=BE=x,
在△ABE和△EHC中,
$\left\{\begin{array}{l}{∠AEB=∠ECH}\\{∠B=∠EHC}\\{AB=EH=2}\end{array}\right.$,
∴△ABE≌△EHC,
∴BE=CH=x,
在Rt△EHC中,∵EH2+CH2=EC2,
∴22+x2=(3-x)2,
∴x=$\frac{5}{6}$,即DF=$\frac{5}{6}$,
故选B.
点评 本题考查矩形的性质、全等三角形的判定和性质、勾股定理.平行四边形的判定和性质等知识,解题的关键是学会添加常用辅助线构造全等三角形解决问题学会利用勾股定理构建方程解决问题,属于中考常考题型.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:解答题
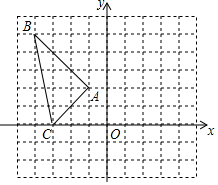 如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,
如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
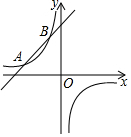 如图,一次函数的图象与反比例函数的图象交于A(-3,1)、B(m,3)两点,
如图,一次函数的图象与反比例函数的图象交于A(-3,1)、B(m,3)两点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
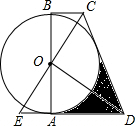 如图,AB为⊙O的直径,BC、AD是⊙O的切线,切点分别为B、A,过点O作EC⊥OD,EC交BC于点C,交AD于点E.
如图,AB为⊙O的直径,BC、AD是⊙O的切线,切点分别为B、A,过点O作EC⊥OD,EC交BC于点C,交AD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动)那么小羊A在草地上的最大活动区域面积是( )
如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动)那么小羊A在草地上的最大活动区域面积是( )| A. | $\frac{17}{12}$π m2 | B. | $\frac{17}{6}$π m2 | C. | $\frac{25}{4}$π m2 | D. | $\frac{77}{12}$π m2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com