
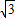 ,0),AC的延长线与⊙B的切线OD交于点D.
,0),AC的延长线与⊙B的切线OD交于点D.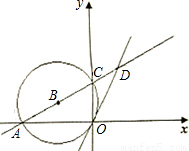
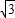 ,0)
,0)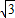
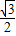
 AC
AC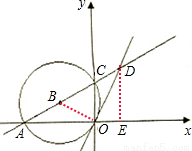
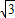
 OD=
OD=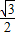 ,在Rt△ODE中,由勾股定理,得
,在Rt△ODE中,由勾股定理,得
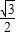 ,
, )
)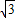 )(x-0),由题意,得
)(x-0),由题意,得 =a(
=a(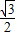 +
+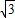 )
)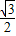 ,解得
,解得
 (x+
(x+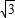 )x
)x x2+
x2+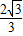 x
x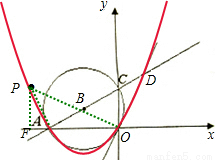
 x2+
x2+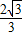 x
x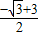 ,x2=
,x2=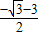
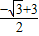 ,1)或(
,1)或(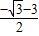 ,1)
,1)

科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).
如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:学习周报 数学 北师大八年级版 2009-2010学年 第19-26期 总第175-182期 北师大版 题型:022
如图,已知甲运动方式为:先竖直向上运动
1个单位长度,再水平向右移动2个单位长度;乙运动方式为:先竖直向下运动2个单位长度,再水平向左移动3个单位长度.在平面直角坐标系内,现有一动点P,第一次从原点O出发按甲方式运动到点P1,第二次从点P1出发按乙方式运动到点P2,第三次从点P2出发再按甲方式运动到点P3,第四次从点P3出发在按乙方式运动到P4,…依此运动规律,则经过第11次运动后,动点P所在位置P11的坐标是________.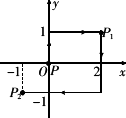
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 相交于点C.
相交于点C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com