
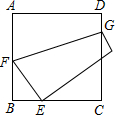
 如图,将正方形ABCD的一角折向边CD,使点A与CB上一点E重合,若BE=1,CE=2,则折痕FG的长度为( )
如图,将正方形ABCD的一角折向边CD,使点A与CB上一点E重合,若BE=1,CE=2,则折痕FG的长度为( )| A. | $\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 4 |
分析 过G作GM⊥AB于M,连接AE,则MG=AD=AB,根据折叠的性质得到AE⊥GF,根据全等三角形的性质得到MF=BE=1,根据勾股定理即可得到结论.
解答  解:过G作GM⊥AB于M,连接AE,
解:过G作GM⊥AB于M,连接AE,
则MG=AD=AB,
∵将正方形ABCD的一角折向边CD,使点A与CB上一点E重合,
∴AE⊥GF,
∴∠FAE+∠AFG=∠AFG+∠MGF,
∴∠BAE=∠MGF,
在△ABE与△MGF中$\left\{\begin{array}{l}{∠B=∠GMF}\\{AB=GM}\\{∠MGF=∠BAM}\end{array}\right.$,
∴△ABE≌△GMF,
∴MF=BE=1,
∵MG=AD=BC=3,
∴FG=$\sqrt{F{M}^{2}+M{G}^{2}}$=$\sqrt{10}$,
故选A.
点评 此题主要考查了图形的翻折变换,根据图形折叠前后图形不发生大小变化得出三角形的全等是解决问题的关键,难度一般.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:选择题
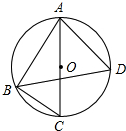 如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )
如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )| A. | 95° | B. | 90° | C. | 85° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为( )
如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为( )| A. | (1345,0) | B. | (1345,$\frac{\sqrt{3}}{2}$) | C. | (1345.5,0) | D. | (1345.5,$\frac{\sqrt{3}}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
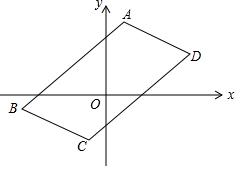 图中的A(1,4),B(-5,-1),C(-1,-3)和D(5,2)是一个平行四边形的顶点
图中的A(1,4),B(-5,-1),C(-1,-3)和D(5,2)是一个平行四边形的顶点查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
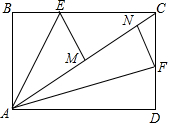 如图,矩形ABCD,将它分别沿AE和AF折叠,恰好使点B,C落到对角线AC上点M,N处,已知MN=2,NC=1,则矩形ABCD的面积是9+2$\sqrt{6}$.
如图,矩形ABCD,将它分别沿AE和AF折叠,恰好使点B,C落到对角线AC上点M,N处,已知MN=2,NC=1,则矩形ABCD的面积是9+2$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明一家人春节期间参与了“支付宝集五福”活动,小明和姐姐都缺一个“敬业福”,恰巧爸爸有一个可以送给其中一个,两个人各设计了一个游戏,获胜者得到“敬业福”,请用适当的方法说明这两个游戏对小明和姐姐是否公平.
小明一家人春节期间参与了“支付宝集五福”活动,小明和姐姐都缺一个“敬业福”,恰巧爸爸有一个可以送给其中一个,两个人各设计了一个游戏,获胜者得到“敬业福”,请用适当的方法说明这两个游戏对小明和姐姐是否公平.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com