
 如图,BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若AD平分∠BAC,试说明:BD=CD.
如图,BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若AD平分∠BAC,试说明:BD=CD. 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
 如图,在梯形ABCD中,AD∥BC,∠B=90°,E是AB的中点,且DC=AD+BC,则下列结论中错误的有( )
如图,在梯形ABCD中,AD∥BC,∠B=90°,E是AB的中点,且DC=AD+BC,则下列结论中错误的有( )| A、DE平分∠ADC |
| B、△DEC是直角三角形 |
| C、点E到DC的距离为AB长的一半 |
| D、△DEC的面积为△ADE面积的2倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:
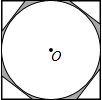 已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )
已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )A、32
| ||
B、
| ||
| C、1 | ||
| D、16-4π |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 上海世博会中国馆共分为国家馆和地区馆两部分,国家馆居中升起、层叠出挑,采用极富中国建筑文化元素的红色“斗冠”造型,由地下一层、地上六层组成.小明通过上网查阅资料得知,国家馆地上六层均为正方形,如图所示,最上面一层正方形边长为a米,以下每层的边长比上一层减少b米.
上海世博会中国馆共分为国家馆和地区馆两部分,国家馆居中升起、层叠出挑,采用极富中国建筑文化元素的红色“斗冠”造型,由地下一层、地上六层组成.小明通过上网查阅资料得知,国家馆地上六层均为正方形,如图所示,最上面一层正方形边长为a米,以下每层的边长比上一层减少b米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com