
【题目】如图,在△ABC中,AB=AC,CE平分∠ACB交AB于点E,CE=BC.
(1)求∠A的度数;
(2)能否在AC边上找一点D,并连接ED,使△AED≌△CEB?若能,请作出你找的点,并证明;若不能,请说明理由.

【答案】(1)36°;(2)见解析.
【解析】
(1)根据等腰三角形的性质,三角形内角和定理和角平分线的性质即可解答本题;
(2)根据(1)中的结论和全等三角形的判定即可解答.
解:(1)∵在△ABC中,AB=AC,
∴∠B=∠ACB,
∵CE平分∠ACB交AB于点E,CE=BC,
∴∠ECA=∠ECB,∠B=∠CEB,
∴∠CEB=∠ACB,
∵∠CEB=∠A+∠ECA,
∴∠A=∠ECA,
设∠A=x,则∠B=∠ACB=2x,
x+2x+2x=180°,
解得,x=36°,
∴∠A=36°;
(2)在AC边上存在一点D,并连接ED,使△AED≌△CEB,作ED∥BC交AC于点D,点D即为所求,
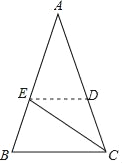
证明:由(1)知∠A=∠ECA,
∴AE=EC,
∵ED∥BC,
∴∠AED=∠B,
∴∠AED=∠CEB,
在△AED和△CEB中,
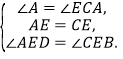
∴△AED≌△CEB(ASA).
故答案为:(1)36°;(2)见解析.


科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(3,4),C(4,﹣1).
(1)试在平面直角坐标系中,画出△ABC;
(2)直接写出△ABC的面积_________
(3)若△A1B1C1与△ABC关于x轴对称,直接写出A1、B1、C1的坐标___________________________________
(4)在x轴上找到一点P,使点P到点A、B两点的距离和最小;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列视图问题
(1)如图(一),它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(2)如图(二),请你借助图四虚线网格画出该几何体的俯视图.
(3)如图(三),它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助图四虚线网格画出该几何体的主视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )
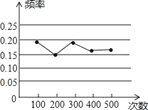
A. 在装有1个红球和2个白球(除颜色外完全相同)的不透明袋子里随机摸出一个球是“白球”
B. 从一副扑克牌中任意抽取一张,这张牌是“红色的”
C. 掷一枚质地均匀的硬币,落地时结果是“正面朝上”
D. 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若AD∥BC,AB∥DE,DF∥AC,∠OEC=72°,∠OCE=64°,则∠B=_______,∠F=_______,∠BAD=_______,∠ADF=_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某一景点等候检票的时间,随机调查了部分游客,统计了他们进入该景点等候检票的时间,并绘制成如图表.
等候时间x(min) | 频数(人数) | 频率 |
10≤x<20 | 8 | 0.2 |
20≤x<30 | 14 | a |
30≤x<40 | 10 | 0.25 |
40≤x<50 | b | 0.125 |
50≤x<60 | 3 | 0.075 |
合计 | 40 | 1 |
(1)这里采用的调查方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)表中a= ,b= ,并请补全频数分布直方图;
(3)根据上述图表制作扇形统计图,则“40≤x<50”所在扇形的圆心角度数是 °.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com