
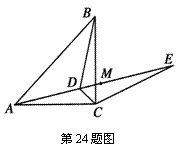
如图24,已知点D为等腰直角△ABC内一点,∠BAD=∠ABD=30°,E为AD延长线上的一点,且CE=CA.
(1)求证:△ADC△BDC
(2)求证:DE平分∠BDC;
(3)若点M在DE上,且DC=DM,求证:ME=BD.
 |
证明:(1)在等腰直角△ABC中, BC=AC
∵∠BAD=∠ABD=30°
∴BD= AD
在△BDC与△ADC中
BC=AC,BD= AD,DC=DC
∴△BDC≌△ADC……………3分
(2)在等腰直角△ABC中
∠BAC=∠ABC=45o
∵∠BAD=∠ABD=30°
∴∠CAD=∠CBD=45o-30o =15o,
∵△ACD≌△BCD
∴∠ACD=∠BCD= 45°
∴∠ADC=∠BDC=180°-15°-45°=120°
∠ADB=360°-120°-120°=120°
∴∠BDE=∠CDE=180°-120°=60°
∴∠BDM=∠EDC,
∴DE平分∠BDC; ……………6分
(3)如图,连接MC,
∵DC=DM,且∠MDC=60°,
∴△MDC是等边三角形,即CM=CD.
又∵∠EMC=180°-∠DMC=180°-60°=120°,
∠ADC=180°-∠MDC=180°-60°=120°,
∴∠EMC=∠ADC. …………………………8分
又∵CE=CA,
∴∠DAC=∠CEM=15°,∴△ADC≌△EMC, ………………………9分
∴ME=AD=DB. ………………………………10分


科目:初中数学 来源: 题型:
如图:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为 ;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com