
“端午节”吃粽子是我国流传了上千年的习俗.某班学生在“端午节”前组织了一次综合实践活动,购买了一些材料制作爱心粽,每人从自己制作的粽子中随机选取两个献给自己的父母,其余的全部送给敬老院的老人们.统计全班学生制作粽子的个数,将制作粽子数量相同的学生分为一组,全班学生可分为A,B,C,D四个组,各组每人制作的粽子个数分别为4,5,6,7.根据如图不完整的统计图解答下列问题:
(1)请补全上面两个统计图;(不写过程)
(2)该班学生制作粽子个数的平均数是 ;
(3)若制作的粽子有红枣馅(记为M)和蛋黄馅(记为N)两种,该班小明同学制作这两种粽子各两个混放在一起,请用列表或画树形图的方法求小明献给父母的粽子馅料不同的概率.
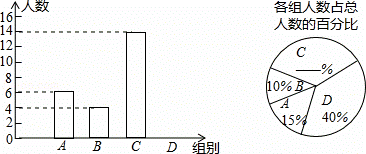
解:(1)根据题意得:6÷15%=40(人),
D的人数为40×40%=16(人),C占的百分比为1﹣(10%+15%+40%)=35%,
补全统计图,如图所示:
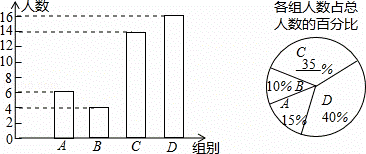
(2)根据题意得:(6×4+4×5+14×6+16×7)÷40=6(个),
则该班学生制作粽子个数的平均数是6个;
故答案为:6个;
(3)列表如下:
| M | M | N | N | |
| M | ﹣﹣﹣ | (M,M) | (N,M) | (N,M) |
| M | (M,M) | ﹣﹣﹣ | (N,M) | (N,M) |
| N | (M,N) | (M,N) | ﹣﹣﹣ | (N,N) |
| N | (M,N) | (M,N) | (N,N) | ﹣﹣﹣ |
所有等可能的情况有12种,其中粽子馅料不同的结果有8种,
则P=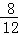 =
=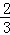 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
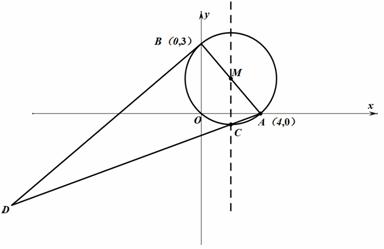
如图,在平面直角坐标系中,⊙M过原点O,与x轴交于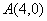 ,与y轴交于
,与y轴交于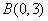 ,点C为劣弧
,点C为劣弧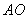 的中点,连接AC并延长到D,使
的中点,连接AC并延长到D,使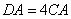 ,连接BD.
,连接BD.
(1) 求⊙M的半径;
求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使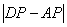 最大.
最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
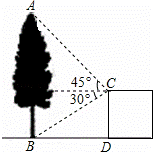
如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为 m(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
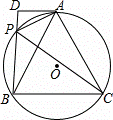
如图,A,P,B,C是⊙O上的四个点,∠APC=∠BPC=60°,过点A作⊙O的切线交BP的延长线于点D.
(1)求证:△ADP∽△BDA;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)若AD=2,PD=1,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场购进一批服装,每件进价为200元,由于换季滞销,商场决定将这种服装按标价的六折销售,若打折后每件服装仍能获利20%,则该服装标价是( )
|
| A. | 350元 | B. | 400元 | C. | 450元 | D. | 500元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
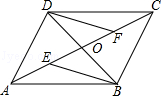
如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若OD=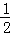 AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com