
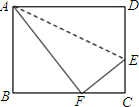
 如图,折叠长方形的一边AD,使点D落在BC边上的F点处,若AB=8cm,BC=10cm,则EC长为3cm.
如图,折叠长方形的一边AD,使点D落在BC边上的F点处,若AB=8cm,BC=10cm,则EC长为3cm.  金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| 图形 |  |  |  |
| 横截线条数 | 0 | 1 | 2 |
| 三角形个数 | 6 |
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2-5ax+4(a<0)经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
如图,抛物线y=ax2-5ax+4(a<0)经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 张莹同学把自己一周的支出情况,用如图所示的统计图表示,则从图中可以看出( )
张莹同学把自己一周的支出情况,用如图所示的统计图表示,则从图中可以看出( )| A. | 一周支出的总金额 | B. | 一周中各项支出所占的百分比 | ||
| C. | 一周各项支出的金额 | D. | 各项支出在一周中的变化情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2+bx+c与x轴分别交于点A(-3,0)和点B,与y轴交于点C(0,3),顶点为点D,对称轴DE交x轴于点E,连接AD,AC,DC.
如图,抛物线y=-x2+bx+c与x轴分别交于点A(-3,0)和点B,与y轴交于点C(0,3),顶点为点D,对称轴DE交x轴于点E,连接AD,AC,DC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<b,则|a|<|b| | B. | a>b,则|a|>|b| | C. | a=b,则|a|=|b| | D. | a≠b,则|a|≠|b| |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果a、b互为相反数,则a+b=0 | B. | a为任意有理数,则它的倒数为$\frac{1}{a}$ | ||
| C. | $\frac{πx{y}^{2}}{7}$的系数是$\frac{π}{7}$ | D. | $\sqrt{81}$的算术平方根是3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com