

分析 (1)根据三角形内角和定理,即可得到∠A1BC+∠A1CB的度数,再根据角平分线的定义,即可得到∠A2BC+∠A2CB的度数,最后根据三角形内角和定理计算即可;
(2)根据三角形内角和定理,即可得到∠A1BC+∠A1CB的度数,再根据BAn、CAn分别是∠A1BC和∠A1CB的n等分线,即可得到∠AnBC+∠AnCB的度数,最后根据三角形内角和定理进行计算即可;
(3)根据∠MBAn+∠NCAn=$\frac{1}{2}$(180°-∠A1)+∠An,以及∠A1=n∠An-180°n+180°,即可得到∠MBAn+∠NCAn=90°n-$\frac{n-2}{2}$∠An,进而变形得出2(∠MBAn+∠NCAn)+(n-2)∠An=180°n.
解答 解:(1)∵∠A1=70°,
∴∠A1BC+∠A1CB=180°-70°=110°,
∵BA2、CA2分别是∠A1BC和∠A1CB的角平分线,
∴∠A2BC+∠A2CB=$\frac{1}{2}$×110°=55°,
∴∠A2=180°-55°=125°.
(2)在△A1BC中,∠A1BC+∠A1CB=180°-α,
∵∠AnBC=$\frac{1}{n}$∠A1BC,∠AnCB=$\frac{1}{n}$∠A1CB,
∴∠AnBC+∠AnCB=$\frac{1}{n}$(∠A1BC+∠A1CB)=$\frac{1}{n}$(180°-α),
∴∠An=180°-(∠AnBC+∠AnCB)=180°-$\frac{1}{n}$(180°-α);
(3)2(∠MBAn+∠NCAn)+(n-2)∠An=180°n.
理由:如图②,∵BM、CN分别是△A1BC的两个外角的角平分线,
∴∠MBE=$\frac{1}{2}$∠A1BE=$\frac{1}{2}$(180°-∠A1BC),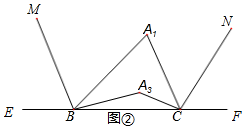
∠NCF=$\frac{1}{2}$∠A1CF=$\frac{1}{2}$(180°-∠A1CB),
∴∠MBAn+∠NCAn=360°-(∠MBE+∠NCF)-(∠AnBC+∠AnCB)
=360°-$\frac{1}{2}$(180°-∠A1BC)-$\frac{1}{2}$(180°-∠A1CB)-(180°-∠An)
=$\frac{1}{2}$(∠A1BC+∠A1CB)+∠An
=$\frac{1}{2}$(180°-∠A1)+∠An
由(2)可得,∠An=180°-$\frac{1}{n}$(180°-∠A1),
∴∠A1=n∠An-180°n+180°,
∴∠MBAn+∠NCAn=$\frac{1}{2}$(180°-n∠An+180°n-180°)+∠An
=90°n-$\frac{n-2}{2}$∠An
∴2(∠MBAn+∠NCAn)+(n-2)∠An=180°n.
点评 本题主要考查了三角形内角和定理以及角平分线的定义的运用,解题时注意:三角形内角和为180°,解答的关键是沟通三角形的外角和内角的数量关系.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
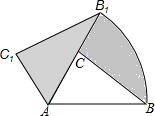 如图,在△ABC中,∠BAC=50°,AC=2,AB=3.现将△ABC绕A点逆时旋转50°得到△AB1C1,则图中的阴影部分的面积为$\frac{5}{4}$π.
如图,在△ABC中,∠BAC=50°,AC=2,AB=3.现将△ABC绕A点逆时旋转50°得到△AB1C1,则图中的阴影部分的面积为$\frac{5}{4}$π.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com