练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．如图，点E在AB上，点F在AC上，且AE=AF，AB=AC，BF=5，DE=1，则DC的长为（　　）
    A．1B．2C．3D．4

    分析 根据AE=AF，AB=AC和∠BAF=∠CAE证明△BAF≌△CAE，进而得到BF=DE，利用CD=CE-DE=BF-DE即可求出答案．

    解答 解：在△BAF和△CAE中，
    $\left\{\begin{array}{l}{AF=AE}\\{∠BAF=∠CAE}\\{AC=AB}\end{array}\right.$，
    ∴BAF≌△CAE（SAS），
    ∴BF=CE，
    ∵BF=5，DE=1，
    ∴CD=CE-DE=BF-DE=5-1=4，
    故选D．

    点评 本题主要考查了全等三角形的判定与性质的知识，解答本题的关键是利用SAS证明△BAF≌△CAE，此题难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．已知m、n是方程2x2-6x+3=0的两根．
    （1）m+n=3；
    （2）mn=$\frac{3}{2}$；
    （3）计算：$\frac{1}{m}$+$\frac{1}{n}$；
    （4）计算：m2+n2；
    （5）计算：$\frac{m}{n}$+$\frac{n}{m}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．x取什么值时，一次函数y1=$\frac{2（2-x）}{3}$-x的值不大于一次函数y2=$\frac{8}{3}$-$\frac{1-3x}{5}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．若x-1是125的立方根，则x-7的立方根是-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知a（a-1）+（b-a2）=8，求$\frac{{a}^{2}+{b}^{2}}{2}-ab$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

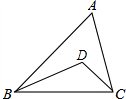    9．如图，在△ABC中，∠ABC和∠ACB的角平分线交于点D．
    （1）如果∠ABC+∠ACB=130°，那么∠BDC=115°；
    （2）如果∠A=50°，那么∠BDC=115°=90°+$\frac{1}{2}$∠A；
    （3）如果∠A=n°，那么∠BDC=90°+$\frac{1}{2}$n°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，抛物线y=-x2+bx+c交x轴于A（-1，0），B（3，0）两点，交y轴于点C，过点C作x轴的平行线与抛物线交于点D．
    （1）求抛物线的解析式；
    （2）点P在x轴上，以A、P、C、D为顶点的四边形是平行四边形，求此时点P的坐标；
    （3）若⊙M的半径为1，圆心M在抛物线上运动，当⊙M与y轴相切时，求⊙M上的点到点C的最短距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．某男子篮球国家队为备战“第十八届男蓝世锦赛”，选拔一名“得分后卫”，队里这个位置上的人选有甲、乙二人，两个队员在教练规定的5个定点进行投篮比赛（这5个定点到篮筐距离均相等），每个定点投篮10次，现对每个定点的进球个数进行统计，小刚依据统计数据绘制了如图所示尚不完整的统计图表．
    球员甲、乙进球成绩统计表
     定点A定点B定点C定点D定点E
    球员甲成绩867410
    球员乙成绩7876a
    小刚的计算结果
     平均数方差
    球员甲74
    （1）观察球员乙投篮进球数的扇形统计图（图1），回答：
    ①乙球员5个定点投篮进球数的众数是7，中位数是7；
    ②进球数为7的扇形所对的圆心角是216°
    （2）a=7，$\overline{x{\;}_{乙}}$=7．
    （3）请完成图2中表示乙成绩变化情况的折线图；
    （4）①观察图2，可以看出乙的成绩比较稳定（填“甲”或“乙”），计算乙成绩的方差，并验证你的判断．
    ②请你从平均数的方差的角度分析，谁将被选中．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，在等边三角形ABC中，BD是AC边上的中线，延长BC到E，使CE=CD．问：
    （1）DB与DE相等吗？
    （2）把BD是AC边上的中线改成什么条件，还能得到同样的结论？

    查看答案和解析>>

    同步练习册答案