
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°. 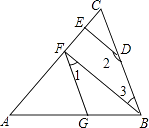
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
【答案】
(1)解:(1)BF∥DE,理由如下:
∵∠AGF=∠ABC,
∴GF∥BC,
∴∠1=∠3,
∵∠1+∠2=180°,
∴∠3+∠2=180°,
∴BF∥DE;
(2)解:∵BF∥DE,BF⊥AC,
∴DE⊥AC,
∵∠1+∠2=180°,∠2=150°,
∴∠1=30°,
∴∠AFG=90°﹣30°=60°.
【解析】(1)由于∠AGF=∠ABC,可判断GF∥BC,则∠1=∠3,由∠1+∠2=180°得出∠3+∠2=180°判断出BF∥DE;(2)由BF∥DE,BF⊥AC得到DE⊥AC,由∠2=150°得出∠1=30°,得出∠AFG的度数
【考点精析】利用余角和补角的特征和垂线的性质对题目进行判断即可得到答案,需要熟知互余、互补是指两个角的数量关系,与两个角的位置无关;垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某电冰箱厂每个月的产量都比上个月增长的百分数相同.已知该厂今年4月份的电冰箱产量为5万台,6月份比5月份多生产了12000台,求该厂今年产量的月平均增长率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①35=3×3×3×3×3;②﹣1是单项式,且它的次数为1;③若∠1=90°﹣∠2,则∠1与∠2互为余角;④对于有理数n、x、y(其中xy≠0),若 ![]() =
= ![]() ,则x=y.其中不正确的有( )
,则x=y.其中不正确的有( )
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
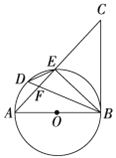
【题目】如图,AB是⊙O的直径,点D是弧AE上一点,且∠BDE=∠CBE,BD与AE交于点F.
(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:DE2=DF·DB;
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B. 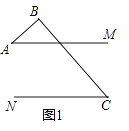
(1)如图1,直接写出∠A和∠C之间的数量关系;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() .下列结论:
.下列结论:
①△ADE∽△ACD; ②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD为8; ④0<CE≤6.4.

其中正确的结论是____________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F分别是BC,AD上的点,且BE=DF,对角线AC⊥AB. 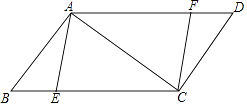
(1)求证:四边形AECF是平行四边形;
(2)①当E为BC的中点时,求证:四边形AECF是菱形;
(3)②若AB=6,BC=10,当BE长为时,四边形AECF是矩形. ③四边形AECF有可能成为正方形吗?答: . (填“有”或“没有”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com