
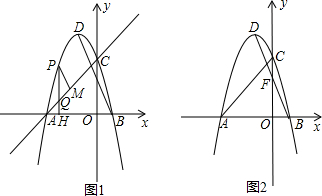
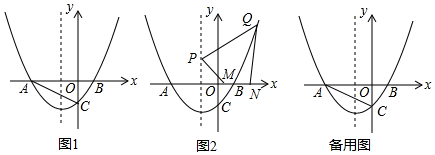
���� ��1�����������������������Ľ��㣬���ô���ϵ�����Լ��䷽�����ɽ�����⣮
��2��������ͼ1�У���DN��y��J��AC��N��ֱ��BD��AC��K���������DKN�����ߣ������PQ�����ֵ���������������ε��������PM��MQ���ɽ�����⣮
����ͼ2�У���PE��x�ύy����E����E����x��ĶԳƵ�K������DK��x�ύ�ڵ�O�䣬��OHƽ�Ƶ�O��H������ʱ�ı���PHO��D���ܳ���С���ֱ����PD��DK��OO�伴�ɽ�����⣮
��3��������������ͼ3�У�����CGK=90��ʱ����OE��GK��E����취�����G���꼴�ɣ�����ͼ4�У�����CKG=90��ʱ�������G���꼴�ɽ�����⣮
��� �⣺��1������������y=-x2-2x+3����x=0��y=3�����C��0��3����
��y=0��-x2-2x+3=0�����x=-3��1��
��A��-3��0����B��1��0����
��ֱ��AC�Ľ���ʽΪy=kx+b����A��C�����������õ�$\left\{\begin{array}{l}{b=3}\\{-3k+b=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪy=x+3��
��y=-x2-2x+3=-��x+1��2+4��
�ඥ��D����Ϊ��-1��4����
��2������ͼ1�У���DN��y��J��AC��N��ֱ��BD��AC��K��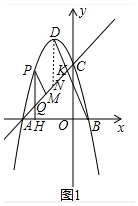
��ֱ��AC�Ľ���ʽΪy=x+3��ֱ��BD�Ľ���ʽΪy=y=-2x+2��
��$\left\{\begin{array}{l}{y=-2x+2}\\{y=x+3}\end{array}\right.$���$\left\{\begin{array}{l}{x=-\frac{1}{3}}\\{y=\frac{8}{3}}\end{array}\right.$��
���K���꣨-$\frac{1}{3}$��$\frac{8}{3}$����N��-1��2����
��DN=2��DK=$\sqrt{��-\frac{1}{3}+1��^{2}+��\frac{8}{3}-4��^{2}}$=$\frac{2\sqrt{5}}{3}$��KN=$\sqrt{��-\frac{1}{3}+1��^{2}+��\frac{8}{3}-2��^{2}}$=$\frac{2\sqrt{2}}{3}$��
�ڡ�PMQ�У��ߡ�PMQ=��DKN=��ֵ��
�൱��PMQ�ܳ������ֵʱ��PQ��ֵ�����P��m��-m2-2m+3����Q��m��m+3����
��PQ=-m2-2m+3-m-3=-m2-3m=-��m+$\frac{3}{2}$��2+$\frac{9}{4}$��
��a=-1��0��
��m=-$\frac{3}{2}$ʱ��PQ�����ֵΪ$\frac{9}{4}$��
�ɡ�PMQ�ס�DKN����$\frac{PM}{DK}$=$\frac{MQ}{KN}$=$\frac{PQ}{DN}$��
��$\frac{PM}{\frac{2\sqrt{5}}{3}}$=$\frac{MQ}{\frac{2\sqrt{2}}{3}}$=$\frac{\frac{9}{4}}{2}$��
��PM=$\frac{3\sqrt{5}}{4}$��MQ=$\frac{3\sqrt{2}}{4}$��
���PMQ���ܳ����ֵΪ$\frac{9}{4}$+$\frac{3\sqrt{5}}{4}$+$\frac{3\sqrt{2}}{4}$��
����ͼ2�У���PE��x�ύy����E����E����x��ĶԳƵ�K������DK��x�ύ�ڵ�O�䣬��OHƽ�Ƶ�O��H������ʱ�ı���PHO��D���ܳ���С��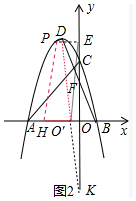
��P��-$\frac{3}{2}$��$\frac{15}{4}$����D��-1��4����K��0��-$\frac{15}{4}$����
��O��������-$\frac{15}{31}$��0����PD=$\sqrt{��-\frac{3}{2}+1��^{2}+��\frac{15}{4}-4��^{2}}$=$\frac{\sqrt{5}}{4}$��DK=$\sqrt{��-1��^{2}+��4+\frac{15}{4}��^{2}}$=$\frac{\sqrt{977}}{4}$��O��H=$\frac{3}{2}$��
��OH����ƽ��$\frac{15}{31}$����λ��L����Сֵ=PD+DK+O��H=$\frac{\sqrt{5}}{4}$+$\frac{\sqrt{977}}{4}$+$\frac{3}{2}$��
��3������ͼ3�У�����CGK=90��ʱ����OE��GK��E��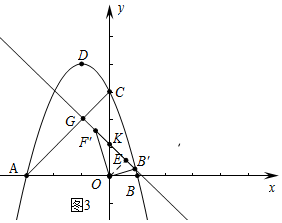
��OA=OC����AOC=90�㣬
���GCK=��GKC=��OKE=��KOE=45�㣬
��OE=$\frac{OB���OF��}{B��F��}$=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$��
��OK=$\frac{2\sqrt{10}}{5}$��KC=3-$\frac{2\sqrt{10}}{5}$��
��G��$\frac{\sqrt{10}}{5}$-$\frac{3}{2}$��$\frac{3}{2}$+$\frac{\sqrt{10}}{5}$����
��GB=$\sqrt{��\frac{\sqrt{10}}{5}-\frac{5}{2}��^{2}+��\frac{3}{2}+\frac{\sqrt{10}}{5}��^{2}}$=$\sqrt{\frac{93}{10}-\frac{2}{5}\sqrt{10}}$��
����ͼ4�У�����CKG=90��ʱ����G��$\frac{2\sqrt{10}}{5}$-3��$\frac{2\sqrt{10}}{5}$����
��BG=$\sqrt{��\frac{2\sqrt{10}}{5}-4��^{2}+��\frac{2\sqrt{10}}{5}��^{2}}$=4$\sqrt{\frac{6-\sqrt{10}}{5}}$��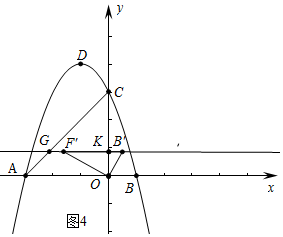
����ͼ5�У�����CGF��=90�㣬ͬ���ɵ�G��-$\frac{\sqrt{10}}{5}$-$\frac{3}{2}$��$\frac{3}{2}$-$\frac{\sqrt{10}}{5}$����
GB=$\sqrt{��\frac{\sqrt{10}}{5}+\frac{5}{2}��^{2}+��\frac{3}{2}-\frac{\sqrt{10}}{5}��^{2}}$=$\sqrt{\frac{93}{10}+\frac{2}{5}\sqrt{10}}$��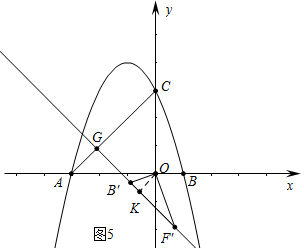 ��
��
����ͼ6�У�����GKC=90�㣬ͬ���ɵ�G��-$\frac{2\sqrt{5}}{5}$-3��-$\frac{2\sqrt{5}}{5}$����
��GB=$\sqrt{��4+\frac{2\sqrt{5}}{5}��^{2}+��\frac{2\sqrt{5}}{5}��^{2}}$=$\sqrt{\frac{88}{5}+\frac{16}{5}\sqrt{5}}$=2$\sqrt{\frac{22}{5}+\frac{4}{5}\sqrt{5}}$��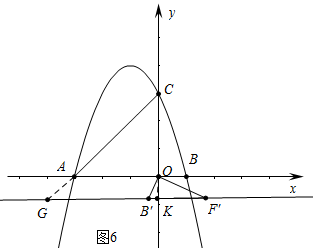
���� ���⿼����κ����ۺ��⡢����ϵ������һ�κ�������Сֵ���⡢��ת�任���������빫ʽ��֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����öԳƽ����ֵ���⣬ѧ���÷������۵�˼��˼�����⣬ѧ�ṹ�����κ���ȷ����ֵ���⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
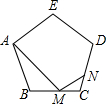 ��ͼ����MΪ�������ABCDE�ı�BC��һ�㣬$\frac{BM}{CM}$=2������AM������AMN=108�㣬MN��CD�ڵ�N����$\frac{CN}{ND}$��ֵΪ$\frac{2}{7}$��
��ͼ����MΪ�������ABCDE�ı�BC��һ�㣬$\frac{BM}{CM}$=2������AM������AMN=108�㣬MN��CD�ڵ�N����$\frac{CN}{ND}$��ֵΪ$\frac{2}{7}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
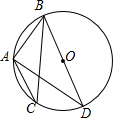 ��ͼ��BD�ǡ�O��ֱ������AB=AC����BAC=120�㣬��֪AB=2����AD=2$\sqrt{3}$��
��ͼ��BD�ǡ�O��ֱ������AB=AC����BAC=120�㣬��֪AB=2����AD=2$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
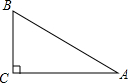 ��ͼ����Rt��ABC�У���C=90�㣬tanA=��������
��ͼ����Rt��ABC�У���C=90�㣬tanA=��������| A�� | $\frac{BC}{AB}$ | B�� | $\frac{AC}{AB}$ | C�� | $\frac{BC}{AC}$ | D�� | $\frac{AC}{BC}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com