
����Ŀ��ijѧУС�����������ǰ40��μ����ʵ�����������һ��������꾭Ӫ���˽һ�ֳɱ�ÿ��20Ԫ������x��������P=50��x���ڵ�x����ۼ�ÿ��yԪ��y��x�Ĺ�ϵ��ͼ��ʾ�� ��֪�����ʵ���ʱ�䳬��һ���y=20+ ![]()

��1���������1��x��20ʱ��y��x�ĺ�����ϵʽ���������12���������۵��ۣ�
��2����40���и��������۴���ڼ����õ�����������������Ƕ��٣�
���𰸡�
��1���⣺��1��x��20ʱ����y=kx+b������1��30.5������20��40������ã�
![]() ��
��
��ã�  ��
��
��y��x�ĺ�����ϵʽΪ��y= ![]() x+30��1��x��20����
x+30��1��x��20����
��x=12ʱ��y=6+30=36��
�𣺺�����ϵʽΪ��y= ![]() x+30����12�����Ʒ�����۵���Ϊÿ��36Ԫ
x+30����12�����Ʒ�����۵���Ϊÿ��36Ԫ
��2���⣺��������x���õ�����ΪwԪ��
��1��x��20ʱ��w=�� ![]() x+30��20����50��x��=��
x+30��20����50��x��=�� ![]() x2+15x+500=��
x2+15x+500=�� ![]() ��x��15��2+
��x��15��2+ ![]() ��
��
�ߩ� ![]() ��0��
��0��
�൱x=15ʱ��w�����ֵw1����w1= ![]() ��
��
��21��x��40ʱ��w=��20+ ![]() ��20����50��x��=
��20����50��x��= ![]() ��315��
��315��
��15750��0��
�� ![]() ��x�����������
��x�����������
��x=21ʱ�� ![]() ���
���
���ǣ�x=21ʱ��w�����ֵw2����w2= ![]() ��315=435��
��315=435��
��w1��w2��
����40���и��������۴����10���õ������������������612.5Ԫ
����������1����1��x��20ʱ����y=kx+b������1��30.5������20��40�����룬���ô���ϵ�������y��x�ĺ�����ϵʽ��Ȼ����ÿ��x��ȡֵ��Χ�ڣ���y=35���ֱ���x��ֵ���ɣ���2����������=�ۼ۩��ɱ����ֱ������1��x��20��21��x��40ʱ����õ�����w��x�ĺ�����ϵʽ�������ö��κ���������������������������ֵ��Ȼ��Ƚϼ��ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ��
�� ![]() ��
�� ![]() ��
��![]() ����
����![]() ��
��
��![]() ����˵��
����˵��![]() �ǵ��������Σ�
�ǵ��������Σ�
��![]() ����֪
����֪![]() ����ͼ
����ͼ![]() ������
������![]() �ӵ�
�ӵ�![]() ������ÿ��
������ÿ��![]() ���ٶ����߶�
���ٶ����߶�![]() ���
���![]() �˶���ͬʱ����
�˶���ͬʱ����![]() �ӵ�
�ӵ�![]() ��������ͬ�ٶ����߶�
��������ͬ�ٶ����߶�![]() ���
���![]() �˶���������һ�㵽���յ�ʱ�����˶���ֹͣ�����
�˶���������һ�㵽���յ�ʱ�����˶���ֹͣ�����![]() �˶���ʱ��Ϊ
�˶���ʱ��Ϊ![]() ���룩��
���룩��
����![]() �ı���
�ı���![]() ƽ�У���
ƽ�У���![]() ��ֵ��
��ֵ��
������![]() �DZ�
�DZ�![]() ���е㣬���ڵ�
���е㣬���ڵ�![]() �˶��Ĺ����У�
�˶��Ĺ����У� ![]() �ܷ��Ϊ���������Σ����ܣ����
�ܷ��Ϊ���������Σ����ܣ����![]() ��ֵ�������ܣ���˵�����ɣ�
��ֵ�������ܣ���˵�����ɣ�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ϣ�С����ѧ��ѧУ���лؼң�����һ�κ�С����ͬѧС��Ҳ��ѧУ�ﳵ�ؼң����С������С����������С�����������г�һ��ؼң������С���ľܾ������С�ѱ��³����Ƴ���С��һ��ؼң��ܿ�С�������ˣ�С����С�������Ҳ���ϳ������ؼң���ѧУ��С���ҡ�С�ѼҶ���ͬһ����ֱ�Ĺ�·�ϣ����С������ʱ����С����С�ѵľ���y����ʱ��t�ĺ���ͼ�����������ͼ�еģ� ����
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
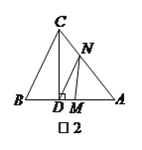
����Ŀ����ͼ������ABC�У�AB=BC��AD��BC�ڵ�D����EΪAC�е���BEƽ�֡�ABD������BE��AD�ڵ�F����BF=AC������D��DG��AB����AC�ڵ�G��
��֤��
��1����BAD=2��DAC
��2��EF=EG��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���A=100�㣬BI��CI�ֱ�ƽ�֡�ABC����ACB�����BIC=________����BM��CM�ֱ�ƽ�֡�ABC����ACB�����ƽ���ߣ����M=__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������и���
��1�����㣺����2��2+�� ![]() ��1��0��
��1��0�� ![]() ����
���� ![]() ����1
����1
��2���� ![]() ��
�� ![]() ����
���� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ı���ABCD�У�����D��DE��AB�ڵ�E����F��CD�ϣ�CF=AE������BF��AF�� 
��1����֤���ı���BFDE�Ǿ��Σ�
��2����AFƽ�֡�BAD����AE=3��DE=4�������BFDE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���˱���ij������������A��ԭ��52ǧ�ˣ�B��ԭ��64ǧ�ˣ�������Щԭ�������ס������ֲ�Ʒ��20������֪����1�����ֲ�Ʒ��ҪA��ԭ��3ǧ�ˣ�B��ԭ��2ǧ�ˣ�����1�����ֲ�Ʒ��ҪA��ԭ��2ǧ�ˣ�B��ԭ��4ǧ�ˣ�����������������Ϊ�� ��
A.4
B.5
C.6
D.7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�Һ���λ�ڵ���P�Ķ������������40 ![]() �����A�����������Ϸ�����һ��ʱ�����λ�ڵ���P����ƫ��30�㷽���ϵ�B����������ʻ��·��ABΪ�� �����
�����A�����������Ϸ�����һ��ʱ�����λ�ڵ���P����ƫ��30�㷽���ϵ�B����������ʻ��·��ABΪ�� ����� 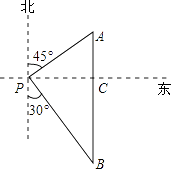
A.40+40 ![]()
B.80 ![]()
C.40+20 ![]()
D.80
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com