
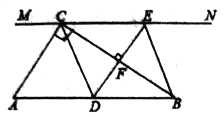
【题目】如图:在Rt△ABC中,∠ACB=90°,过点C的直线MN//AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连结CD,BE.
(1)求点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由.
(2)在(1)的条件下,当∠A= 时,四边形BECD是正方形.说明你的理由.
【答案】(1)平行四边形BECD是菱形,理由见解析;(2)45°
【解析】
(1)先证明AC∥DE,得出四边形BECD是平行四边形,再“根据直角三角形斜边上的中线等于斜边的一半”证出CD=BD,得出四边形BECD是菱形;
(2)先求出∠ABC=45°,再根据菱形的性质求出∠DBE=90°,即可证出结论.
(1)当点D是AB的中点时,四边形BECD是菱形;理由如下:
∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
∵D为AB中点,
∴AD=BD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=![]() AB=BD,
AB=BD,
∴四边形BECD是菱形;
(2)当∠A=45°时,四边形BECD是正方形;理由如下:
∵∠ACB=90°,∠A=45°,
∴∠ABC=45°,
∵四边形BECD是菱形,
∴∠ABC=![]() ∠DBE,
∠DBE,
∴∠DBE=90°,
∴四边形BECD是正方形.
故答案为:45°.


科目:初中数学 来源: 题型:
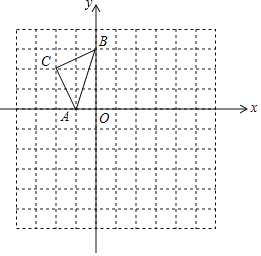
【题目】如图,在已知的平面直角坐标系中,△ABC的顶点都在正方形网格的格点上,若A,B两点的坐标分别是A(-1,0),B(0,3).
(1)将△ABC绕原点O顺时针旋转90°得到△A1B1C1,画出△A1B1C1;
(2)以点O为位似中心,与△ABC位似的△A2B2C2满足A2B2:AB=2:1,请在网格内画出△A2B2C2,并直接填写△A2B2C2的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
1637 年笛卡儿(R.Descartes,1596 1650)在其《几何学》中,首次应用待定系数法将 4 次方程分解为两个 2 次方程求解,并最早给出因式分解定理.
他认为,若一个高于二次的关于 x 的多项式能被 (![]() ) 整除,则其一定可以分解为 (
) 整除,则其一定可以分解为 (![]() ) 与另外一个整式的乘积,而且令这个多项式的值为 0 时, x = a 是关于 x 的这个方程的一个根.
) 与另外一个整式的乘积,而且令这个多项式的值为 0 时, x = a 是关于 x 的这个方程的一个根.
例如:多项式![]() 可以分解为 (
可以分解为 (![]() ) 与另外一个整式 M 的乘积,即
) 与另外一个整式 M 的乘积,即 ![]()
令![]() 时,可知 x =1 为该方程的一个根.
时,可知 x =1 为该方程的一个根.
关于笛卡尔的“待定系数法”原理,举例说明如下: 分解因式:![]()
观察知,显然 x=1 时,原式 = 0 ,因此原式可分解为 (![]() ) 与另一个整式的积.
) 与另一个整式的积.
令:![]() ,则
,则![]() =
=![]() ,因等式两边 x 同次幂的系数相等,则有:
,因等式两边 x 同次幂的系数相等,则有: ,得
,得![]() ,从而
,从而![]()
此时,不难发现 x= 1 是方程 ![]() 的一个根.
的一个根.
根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)若![]() 是多项式
是多项式![]() 的因式,求 a 的值并将多项式
的因式,求 a 的值并将多项式![]() 分解因式;
分解因式;
(2)若多项式![]() 含有因式
含有因式![]() 及
及![]() ,求a+ b 的值.
,求a+ b 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进冰箱、彩电进行销售.相关信息如下表:
进价(元/台) | 售价(元/台) | |
冰箱 |
| 2500 |
彩电 |
| 2000 |
(1)若商场用80000元购进冰箱的数量与用64000元购进彩电的数量相等,求表中a的值.
(2)为了满足市场需要求,商场决定用不超过9万元采购冰箱、彩电共50台,且冰箱的数量不少于彩电数量的![]() .
.
①该商场有哪几种进货方式?
②若该商场将购进的冰箱、彩电全部售出,获得的最大利润为w元,请用所学的函数知识求出w的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种油菜籽在相同条件下的发芽实验结果如表:
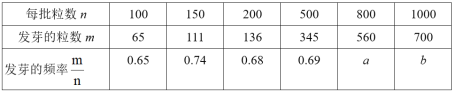
(1)a= ,b= ;
(2)这种油菜籽发芽的概率估计值是多少?请简要说明理由;
(3)如果该种油菜籽发芽后的成秧率为90%,则在相同条件下用10000粒该种油菜籽可得到油菜秧苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形纸片ABCD中,AB=6,BC=8.
(1)将矩形纸片沿BD折叠,点A落在点E处(如图①),设DE与BC相交于点F,求BF的长;
(2)将矩形纸片折叠,使点B与点D重合(如图②),求折痕GH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(+17)+(-12);
(2)10+(―![]() )―6―(―0.25);
)―6―(―0.25);
(3)(![]() )×48 ;
)×48 ;
(4)|-5-4|-5×(-2)2-1÷(-![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com