
 (建筑施工高处作业安全技术规范)(JGJ80-91)规定,折梯(即人字梯)使用时上部夹角以35°-45°为宜,铰链必须牢固,并应有可靠的拉撑措施.如下图所示,小明想在人字梯的A、B处系上一根绳子确保用梯安全,他测得OA=OB=3米,在A、B处打结各需要0.5米的绳子,请你帮小明计算一下,他需要的绳子应该在什么范围内?
(建筑施工高处作业安全技术规范)(JGJ80-91)规定,折梯(即人字梯)使用时上部夹角以35°-45°为宜,铰链必须牢固,并应有可靠的拉撑措施.如下图所示,小明想在人字梯的A、B处系上一根绳子确保用梯安全,他测得OA=OB=3米,在A、B处打结各需要0.5米的绳子,请你帮小明计算一下,他需要的绳子应该在什么范围内?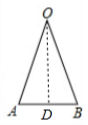 解:作OD⊥AB于D,
解:作OD⊥AB于D, ∠AOB,AD=DB=
∠AOB,AD=DB= AB,
AB, ,
,

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
 如图:在正方形ABCD中,∠EAF=∠EAB,点F在CD边上,∠AEF=90度,联结AE、AF、EF,
如图:在正方形ABCD中,∠EAF=∠EAB,点F在CD边上,∠AEF=90度,联结AE、AF、EF,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,求CF的长.
,求CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com