
【题目】在一条平坦的公路旁边建造了A,B两栋住房,这两栋住房与小明所就读的西湖中学在同一条直线上,如图,已知A栋住房有6层,每层高4 m;B栋住房共3层,每层也是4 m,且A,B两栋楼相距30 m,小明家住在A栋楼的第5层,放学后,小明从学校向这两栋楼走来.
问:(1)小明离B栋楼多远时,他才能完全看不到他家的那层楼房?
(2)小明要想完全看到他家的那层楼房,他离B栋楼的距离要满足什么条件(小明的身高不计)?

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图在△ABC中,BF、CF是角平分线,DE∥BC,分别交AB、AC于点D、E,DE经过点F.结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE; ③△ADE的周长=AB+AC;④BF=CF.其中正确的是______.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B![]() 90°,AB
90°,AB![]() 4,BC
4,BC![]() 2,以AC为边作△ACE,∠ACE
2,以AC为边作△ACE,∠ACE![]() 90°,AC=CE,延长BC至点D,使CD
90°,AC=CE,延长BC至点D,使CD![]() 5,连接DE.求证:△ABC∽△CED.
5,连接DE.求证:△ABC∽△CED.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD,∠BAD的平分线交BC于E,连接DE.
(1)说明点D在△ABE的外接圆上;
(2)若∠AED=∠CED,试判断直线CD与△ABE外接圆的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】腰长为4的等腰直角![]() 放在如图所示的平面直角坐标系中,点A、C均在y轴上,C(0,2),∠ACB=90
放在如图所示的平面直角坐标系中,点A、C均在y轴上,C(0,2),∠ACB=90![]() ,AC=BC=4,平行于y轴的直线x=-2交线段AB于点D,点P是直线x=-2上一动点,且在点D的上方,当
,AC=BC=4,平行于y轴的直线x=-2交线段AB于点D,点P是直线x=-2上一动点,且在点D的上方,当![]() 时,以PB为直角边作等腰直角
时,以PB为直角边作等腰直角![]() ,则所有符合条件的点M的坐标为________.
,则所有符合条件的点M的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学响应“阳光体育”活动的号召,准备从体育用品商店购买一些排球、足球和篮球,排球和足球的单价相同,同一种球的单价相同,若购买2个足球和3个篮球共需340元,购买4个排球和5个篮球共需600元.
(1)求购买一个足球,一个篮球分别需要多少元?
(2)该中学根据实际情况,需从体育用品商店一次性购买三种球共100个,且购买三种球的总费用不超过6000元,求这所中学最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数![]() (x>0)与正比例函数y=kx、
(x>0)与正比例函数y=kx、 ![]() (k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
(k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H.易证∠EHF=∠EGF=∠GEH=90°,从而可知四边形EGFH是矩形.
小明继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请在下列框中补全他的证明思路.
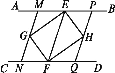
由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形.要证平行四边形MNQP是菱形,只要证MN=NQ.由已知条件_____,MN∥EF,可得NG=NF,故只要证GM=FQ,即证△MGE≌△QFH.易证_____,_____,故只要证∠MGE=∠QFH,易证∠MGE=∠GEF,∠QFH=∠EFH,_____,即可得证.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
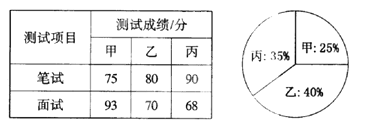
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如扇形图所示,每得一票记作1分.
(l)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到 0.01 )?
(2)根据实际需要,单位将笔试、面试、民主评议三项测试得分按5 : 2 : 3的比例确定个人成绩,那么谁将被录用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com