
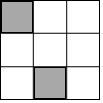
 如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,能使三个被涂黑的小正方形组成一个轴对称图形的概率是( )
如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,能使三个被涂黑的小正方形组成一个轴对称图形的概率是( )| A. | $\frac{5}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{2}{7}$ |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
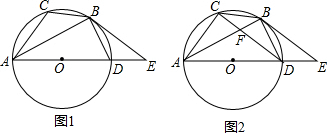
 如图,已知直线l1:y=-2x+8与双曲线C:y=$\frac{6}{x}$(x>0),相交于点A和B(点A在点B的左上方),直线l2:y=kx(k>0)与直线l1相交于点C,于双曲线C相交于点D.(1)求点A、B的坐标;
如图,已知直线l1:y=-2x+8与双曲线C:y=$\frac{6}{x}$(x>0),相交于点A和B(点A在点B的左上方),直线l2:y=kx(k>0)与直线l1相交于点C,于双曲线C相交于点D.(1)求点A、B的坐标;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
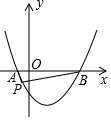 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )| A. | -1<m<0 | B. | -1<m<0或3<m<4 | C. | 0<m<3或m>4 | D. | m<-1或0<m<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知点M(2,-3)、N(6,-3),连接MN,如果点P在直线y=-x+1上,且点P到直线MN的距离不小于1,那么称点P是线段MN的“疏远点”.
如图,在平面直角坐标系中,已知点M(2,-3)、N(6,-3),连接MN,如果点P在直线y=-x+1上,且点P到直线MN的距离不小于1,那么称点P是线段MN的“疏远点”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①②④ | C. | ①② | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A、B、C、D、E的坐标分别是(0,a)、(-3,2)、(b,m)、(-b,m),则点E的坐标是( )
如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A、B、C、D、E的坐标分别是(0,a)、(-3,2)、(b,m)、(-b,m),则点E的坐标是( )| A. | (2,-3) | B. | (2,3) | C. | (3,2) | D. | (3,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com