

| Ė®ŅųÖłµÄ³¤¶Čx£Øcm£© | 4.0 | ” | 8.0 | 9.6 |
| ĢåĪĀ¼ĘµÄ¶ČŹży£Ø”ę£© | 35.0 | ” | 40.0 | 42.0 |
·ÖĪö £Ø1£©øł¾Ż±ķøńÖŠµÄŹż¾ŻĄūÓĆ“ż¶ØĻµŹż·Ø£¬¼“æÉĒó³öy¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©½«x=6.0“śČė£Ø1£©µÄ½įĀŪÖŠĒó³öyÖµ¼“æÉ£®
½ā“š ½ā£ŗ£Ø1£©Éčy¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½ĪŖy=kx+b£Øk”Ł0£©£¬
½«µć£Ø4£¬35£©”¢£Ø8£¬40£©“śČėy=kx+b£¬
$\left\{\begin{array}{l}{4k+b=35}\\{8k+b=40}\end{array}\right.$£¬½āµĆ£ŗ$\left\{\begin{array}{l}{k=\frac{5}{4}}\\{b=30}\end{array}\right.$£¬
”ąy¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½ĪŖy=$\frac{5}{4}$x+30£®
£Ø2£©µ±x=6.0Ź±£¬y=$\frac{5}{4}$x+30=$\frac{5}{4}$”Į6+30=37.5£®
“š£ŗ“ĖŹ±ĢåĪĀ¼ĘµÄ¶ĮĪŖ37.5”ę£®
µćĘĄ ±¾Ģāæ¼²éĮĖŅ»“ĪŗÆŹżµÄÓ¦ÓĆ”¢“ż¶ØĻµŹż·ØĒóŅ»“ĪŗÆŹż½āĪöŹ½ŅŌ¼°Ņ»“ĪŗÆŹżĶ¼ĻóÉĻµćµÄ×ų±źĢŲÕ÷£¬½āĢāµÄ¹Ų¼üŹĒ£ŗ£Ø1£©øł¾Ż±ķøńÖŠµÄŹż¾ŻĄūÓĆ“ż¶ØĻµŹż·Ø£¬Ēó³öy¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½£»£Ø2£©ĄūÓĆŅ»“ĪŗÆŹżĶ¼ĻóÉĻµćµÄ×ų±źĢŲÕ÷Ēó³öµ±x=6.0Ź±yÖµ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
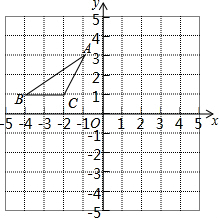 ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬”÷ABCµÄĪ»ÖĆČēĶ¼ĖłŹ¾£¬A”¢B”¢CČżµćµÄ×ų±ź·Ö±šĪŖA£Ø-1£¬3£©”¢B£Ø-4£¬1£©”¢C£Ø-2£¬1£©£¬°Ń”÷ABCĻņÓŅĘ½ŅĘ4øöµ„Ī»³¤¶ČŗóµĆµ½¶ŌÓ¦µÄ”÷A1B1C1£¬ŌŁ½«”÷A1B1C1ĻņĻĀĘ½ŅĘ5øöµ„Ī»³¤¶ČŗóµĆµ½¶ŌÓ¦µÄ”÷A2B2C2£®
ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬”÷ABCµÄĪ»ÖĆČēĶ¼ĖłŹ¾£¬A”¢B”¢CČżµćµÄ×ų±ź·Ö±šĪŖA£Ø-1£¬3£©”¢B£Ø-4£¬1£©”¢C£Ø-2£¬1£©£¬°Ń”÷ABCĻņÓŅĘ½ŅĘ4øöµ„Ī»³¤¶ČŗóµĆµ½¶ŌÓ¦µÄ”÷A1B1C1£¬ŌŁ½«”÷A1B1C1ĻņĻĀĘ½ŅĘ5øöµ„Ī»³¤¶ČŗóµĆµ½¶ŌÓ¦µÄ”÷A2B2C2£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ŅŃÖŖĮāŠĪµÄĮ½Ģõ¶Ō½ĒĻß | B£® | ŅŃÖŖĮāŠĪµÄŅ»±ßŗĶŅ»øöÄŚ½Ē | ||
| C£® | ŅŃÖŖĮāŠĪµÄĖÄ±ß | D£® | ŅŃÖŖĮāŠĪµÄÖܳ¤ŗĶĆ껿 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ³¤·½ŠĪ | B£® | Čż½ĒŠĪ | C£® | ³¤·½ŠĪ»ņÕż·½ŠĪ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com