
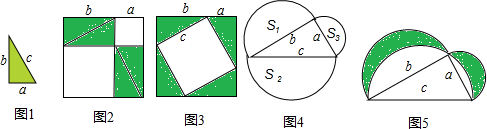
观察图3和图4,分别说出它们由哪些基本图形组成,运用了哪些图形变换?

科目:初中数学 来源: 题型:
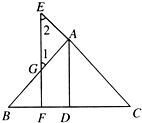 23、已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
23、已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:江苏省镇江市2006年初中毕业、升学统一考试数学试卷 题型:044
小刘对本班同学的业余兴趣爱好进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2.

请你根据图中提供的信息,解答下列问题:
(1)在图1中,将“书画”部分的图形补充完整;
(2)在图2中,求出“球类”部分所对应的圆心角的度数,并分别写出爱好“音乐”、“书画”、“其它”的人数占本班学生数的百分数;
(3)观察图1和图2,你能得出哪些结论?(只要写出一条结论).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com