
(本题12分)
如图,直线 与
与 轴、
轴、 轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动.
动直线EF从
轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动.
动直线EF从 轴开始以每秒1个长度单位的速度向上平行移动(即EF∥
轴开始以每秒1个长度单位的速度向上平行移动(即EF∥ 轴),并且分别与
轴),并且分别与 轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.
轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.

(1)当t=1秒时,求梯形OPFE的面积;
(2)t为何值时,梯形OPFE的面积最大,最大面积是多少?
(3)设t的值分别取t1、t2时(t1≠t2),所对应的三角形分别为△AF1P1和△AF2P2.试判断这两个三角形是否相似,请证明你的判断.
(1)梯形OPFE的面积为18;(2)当t="5" (在0<t<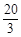 范围内)时,S最大值=50.
范围内)时,S最大值=50.
(3)作FD⊥x轴于D,则四边形OEFD为矩形.
∴FD=OE=t,AF=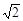 FD=
FD=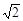 t. 又AP=3t.
t. 又AP=3t.
当t=t1时,AF1=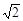 t1,AP1=3t1;当t=t2时,AF2=
t1,AP1=3t1;当t=t2时,AF2=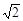 t2,AP2=3t2;
t2,AP2=3t2;
∴ ,又∠A=∠A,∴△AF1P1∽△AF2P2.
,又∠A=∠A,∴△AF1P1∽△AF2P2.
【解析】
试题分析:解:设梯形OPFE的面积为S.
(1) 由直线 与
与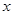 轴、
轴、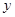 轴分别交于A、B两点
轴分别交于A、B两点
∴A(20,0),B(0,20)
∴OA=OB=20,∠A=∠B=45°..
当t=1时,OE=1,AP=3,∴OP=17,EF=BE=19.
∴S=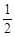 (OP+EF)·OE=18.
(OP+EF)·OE=18.
(2) OE=t,AP=3t,∴OP=20-3t,EF=BE=20-t.
∴S=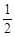 (OP+EF)·OE=
(OP+EF)·OE=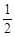 (20-3t +20-t)·t =-2t2+20t=-2(t-5)2+50.
(20-3t +20-t)·t =-2t2+20t=-2(t-5)2+50.
∴当t="5" (在0<t<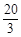 范围内)时,S最大值="50."
范围内)时,S最大值="50."


|
 (3) 作FD⊥x轴于D,则四边形OEFD为矩形.
(3) 作FD⊥x轴于D,则四边形OEFD为矩形.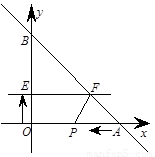
∴FD=OE=t,AF=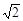 FD=
FD=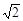 t. 又AP=3t.
t. 又AP=3t.
当t=t1时,AF1=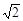 t1,AP1=3t1;当t=t2时,AF2=
t1,AP1=3t1;当t=t2时,AF2=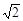 t2,AP2=3t2;
t2,AP2=3t2;
∴ ,又∠A=∠A,∴△AF1P1∽△AF2P2.
,又∠A=∠A,∴△AF1P1∽△AF2P2.
考点:梯形面积公式;动点问题
点评:难题较高。本题考查学生对梯形面积公式的计算,相似三角形判定及动点和动直线作用下图形变化的理解,找出相对应的变量,结合上下题之间能使用的关系式进行计算。要能够在众多条件中准确找出对应所需的信息。


科目:初中数学 来源: 题型:
(本题12分)如图,∠AOB为直角,∠BOC为锐角,且OM平分∠AOC,ON平分∠BOC.
1.⑴若∠BOC=50°,试求∠MON的度数;
2.⑵如果⑴中的∠BOC=α(α为锐角),其他条件不变,试求∠MON的度数;
3.⑶如果⑴中∠AOB=β,其他条件不变,你能求出∠MON的度数吗?
4.⑷从⑴⑵⑶的结果,你能看出什么规律?
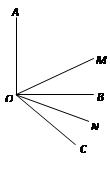
查看答案和解析>>
科目:初中数学 来源: 题型:
、(本题12分)如图,设抛物线C1:![]() ,C2:
,C2: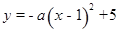 ,C1与C2的交点为A, B,点A的坐标是
,C1与C2的交点为A, B,点A的坐标是![]() ,点B的横坐标是-2.
,点B的横坐标是-2.
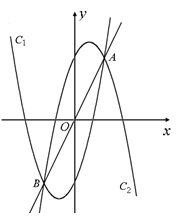
1.(1)求![]() 的值及点B的坐标;
的值及点B的坐标;
2.(2)点D在线段AB上,过D作x轴的垂线,垂足为点H,在DH的右侧作正三角形DHG. 记过C2顶点M的直线为![]() ,且
,且![]() 与x轴交于点N.
与x轴交于点N.
① 若![]() 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
② 若![]() 与△DHG的边DG相交,求点N的横坐标的取值范围.
与△DHG的边DG相交,求点N的横坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
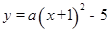 , C2:
, C2: ,C1与C2的交点为A, B,点A的坐标是
,C1与C2的交点为A, B,点A的坐标是 ,点B的横坐标是-2.
,点B的横坐标是-2.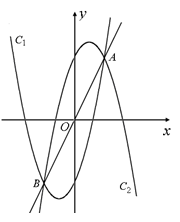
 的值及点B的坐标;
的值及点B的坐标;  ,且
,且 与x轴交于点N.
与x轴交于点N.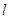 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;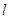 与△DHG的边DG相交,求点N的横坐标的取值范围.
与△DHG的边DG相交,求点N的横坐标的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:
 个不全等的等腰直角三角形OAB和OCD叠放在一起,并且有公共的直角顶点O.
个不全等的等腰直角三角形OAB和OCD叠放在一起,并且有公共的直角顶点O.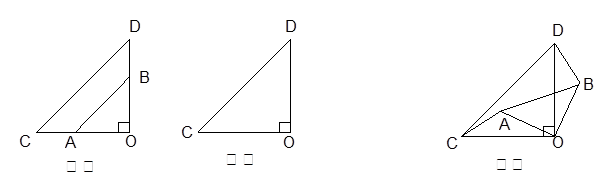
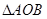 绕点O顺时针旋转
绕点O顺时针旋转 ,在图乙中作出旋转后的
,在图乙中作出旋转后的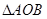 ;
;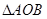 绕点O顺时针旋转一个锐角,得到图丙,这时(1)中的两个结论是否成立?作出判断,并说明理由.若
绕点O顺时针旋转一个锐角,得到图丙,这时(1)中的两个结论是否成立?作出判断,并说明理由.若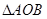 绕点O继续旋转更大的角度时,结论仍然成立吗?作出判断,不必说明理由.
绕点O继续旋转更大的角度时,结论仍然成立吗?作出判断,不必说明理由.查看答案和解析>>
科目:初中数学 来源:2011-2012年浙江省金华市上学期九年级月考数学卷 题型:解答题
、(本题12分)如图,设抛物线C1: ,
C2:
,
C2: ,C1与C2的交点为A, B,点A的坐标是
,C1与C2的交点为A, B,点A的坐标是 ,点B的横坐标是-2.
,点B的横坐标是-2.

1.(1)求 的值及点B的坐标;
的值及点B的坐标;
2.(2)点D在线段AB上,过D作x轴的垂线,垂足为点H,在DH的右侧作正三角形DHG. 记过C2顶点M的直线为 ,且
,且 与x轴交于点N.
与x轴交于点N.
① 若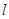 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
② 若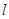 与△DHG的边DG相交,求点N的横坐标的取值范围.
与△DHG的边DG相交,求点N的横坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com