
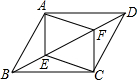
 已知:如图,在?ABCD中,E、F是对角线BD上的两点,且BE=DF,求证:四边形AECF是平行四边形;
已知:如图,在?ABCD中,E、F是对角线BD上的两点,且BE=DF,求证:四边形AECF是平行四边形;分析 连接AC,交BD于点O.由平行四边形的性质得出OA=OC,OB=OD,再结合已知条件证得OE=OF,由“对角线互相平分的四边形是平行四边形”即可得出结论;
变式:由ASA证明△ABE≌△CDF,得出对应边相等BE=DF,得出OE=OF,即可得出结论.
解答 证明:连接AC,交BD于点O.如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
又∵BE=DF,
∴OB-BE=OD-DF,即OE=OF.
又∵OA=OC,
∴四边形AECF是平行四边形.
变式:
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OA=OC,OB=OD,
∴∠ABE=∠CDF.
在△ABE与△CDF中,$\left\{\begin{array}{l}{∠BAE=∠DCF}&{\;}\\{AB=CD}&{\;}\\{∠ABE=∠CDF}&{\;}\end{array}\right.$,
∴△ABE≌△CDF(ASA),
∴BE=DF,
∴OB-BE=OD-DF,
即OE=OF.
又∵OA=OC,
∴四边形AECF是平行四边形.
点评 本题考查了平行四边形的判定与性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,灵活运用平行四边形的判定方法是解决问题的关键.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
 如图,张大爷有一块三角形土地ABC,测得AC=6,BC=12,AB=10,原有一条机耕路AD,且AD⊥BC,现在张大爷想把这条机耕路挖掉,请计算这条机耕路的长度.
如图,张大爷有一块三角形土地ABC,测得AC=6,BC=12,AB=10,原有一条机耕路AD,且AD⊥BC,现在张大爷想把这条机耕路挖掉,请计算这条机耕路的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
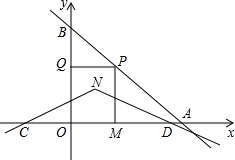 如图,在平面直角坐标系中,直线y=-x+6交x轴于点A,交y轴于点B,点P为直线AB上一动点,过点P作PM⊥x轴于点M,PQ⊥y轴于点Q,点P的横坐标为m,∠CND的两边NC的解析式为y=$\frac{x}{2}$+m-$\frac{1}{2}$,边ND的解析式为y=-$\frac{x}{2}$+m+$\frac{1}{2}$,也随点P的运动而变化,其顶点为点N.
如图,在平面直角坐标系中,直线y=-x+6交x轴于点A,交y轴于点B,点P为直线AB上一动点,过点P作PM⊥x轴于点M,PQ⊥y轴于点Q,点P的横坐标为m,∠CND的两边NC的解析式为y=$\frac{x}{2}$+m-$\frac{1}{2}$,边ND的解析式为y=-$\frac{x}{2}$+m+$\frac{1}{2}$,也随点P的运动而变化,其顶点为点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com