
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | m=-4 | B. | m=-3或-4 | C. | m-3、-4、0或1 | D. | -4<m<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
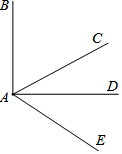 如图,∠BAD=90°,射线AC平分∠BAE.
如图,∠BAD=90°,射线AC平分∠BAE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
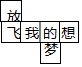 如图,七年级(1)班的学生为节约资源将数学课上正方体展开的图形上写上“放飞我的梦想”,作为班会课横幅,若把这个纸片再折叠成正方体,那么与“放”相对面上的字是梦.
如图,七年级(1)班的学生为节约资源将数学课上正方体展开的图形上写上“放飞我的梦想”,作为班会课横幅,若把这个纸片再折叠成正方体,那么与“放”相对面上的字是梦.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,实数a、b在数轴上的位置,化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$.
如图,实数a、b在数轴上的位置,化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com