
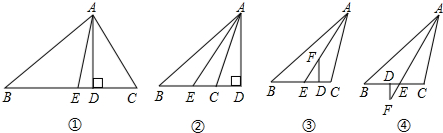
分析 (1)由三角形高的定义得到∠CDA=90°-∠C,再由角平分线定义得到∠CAE=$\frac{1}{2}$∠BAC,接着根据三角形内角和得∠CAE=$\frac{1}{2}$(180°-∠B-∠C)=90°-$\frac{1}{2}$(∠B+∠C),然后计算∠CAE-∠CAD即可得到∠DAE=$\frac{1}{2}$(∠C-∠B);
(2)利用互余得到∠CAD=∠ACB-90°,与(1)一样可得∠CAE=90°-$\frac{1}{2}$(∠B+∠ACB),然后计算∠CAE+∠CAD即可得到∠DAE=$\frac{1}{2}$(∠ACB-∠B);
(3)作AH⊥BC于H,如图③,由(2)得∠HAE=$\frac{1}{2}$(∠ACB-∠B),然后根据平行线的性质易得∠DFE=∠HAE=$\frac{1}{2}$(∠ACB-∠B);
(4)AH⊥BC于H,如图④,和(3)方法一样可得∠DFE=$\frac{1}{2}$(∠ACB-∠B).
解答  解:(1)∵AD是BC边上的高,
解:(1)∵AD是BC边上的高,
∴∠ADC=∠ADE=90°,
∴∠CDA=90°-∠C,
∵AE是∠BAC的平分线,
∴∠CAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠C)=90°-$\frac{1}{2}$(∠B+∠C),
∴∠DAE=∠CAE-∠CAD=90°-$\frac{1}{2}$(∠B+∠C)-(90°-∠C)=$\frac{1}{2}$(∠C-∠B);
(2)成立.
理由如下:∠ADC=90°,
∴∠ACB=90°+∠CDA,
∴∠CAD=∠ACB-90°,
∵AE是∠BAC的平分线,
∴∠CAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠ACB)=90°-$\frac{1}{2}$(∠B+∠ACB),
∴∠DAE=∠CAE+∠CAD=90°-$\frac{1}{2}$(∠B+∠ACB)+(∠ACB-90°)=$\frac{1}{2}$(∠ACB-∠B);
(3)作AH⊥BC于H,如图③,由(2)得∠HAE=$\frac{1}{2}$(∠ACB-∠B);
∵FD⊥BC,
∴FD∥AH,
∴∠DFE=∠HAE=$\frac{1}{2}$(∠ACB-∠B);
(4)AH⊥BC于H,如图④,与(3)一样可得∠DFE=∠HAE=$\frac{1}{2}$(∠ACB-∠B).
点评 本题考查了三角形内角和定理:三角形内角和定理:三角形内角和是180°.也考查了平行线的性质.准确识别图形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
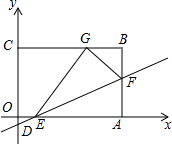 如图,矩形OABC的边OA在x轴上,边OC在y轴上,点B在第一象限,直线y=$\frac{1}{3}$x-1与x轴、y轴、边AB分别交于点E,点D,点F,将△AEF沿直线EF折叠,点A恰好落在BC边的点G位置上,线段AF,BF的长是一元二次方程x2-9x+20=0的两根(AF>BF).
如图,矩形OABC的边OA在x轴上,边OC在y轴上,点B在第一象限,直线y=$\frac{1}{3}$x-1与x轴、y轴、边AB分别交于点E,点D,点F,将△AEF沿直线EF折叠,点A恰好落在BC边的点G位置上,线段AF,BF的长是一元二次方程x2-9x+20=0的两根(AF>BF).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
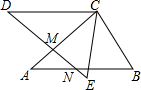 如图,AB=DE,AC=DC,BC=EC,DE与AC、AB分别交于点M、N,CE与AB交于点H,且∠A=∠BCE=40°,∠B=60°
如图,AB=DE,AC=DC,BC=EC,DE与AC、AB分别交于点M、N,CE与AB交于点H,且∠A=∠BCE=40°,∠B=60°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com