
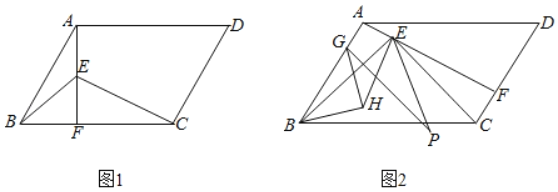
【题目】如图,ABCD中,E为平行四边形内部一点,连接AE,BE,CE.
(1)如图1,AE⊥BC交BC于点F,已知∠EBC=45°,∠BAF=∠ECF,AB=![]() ,EF=1,求AD的长;
,EF=1,求AD的长;
(2)如图2,AE⊥CD交CD于点F,AE=CF且∠BEC=90°,G为AB上一点,作GP⊥BE且GP=CE,并以BG为斜边作等腰Rt△BGH,连接EP、EH.求证:EP=![]() EH.
EH.
【答案】(1)AD=3.(2)见解析.
【解析】
(1)证明△AFB≌△CFE(AAS),推出BF=EF=1,利用勾股定理求出AF即可解决问题.
(2)如图2中,设PG交BE于T,BE交GH于Q.证明△BAE≌△EFC(ASA),推出BE=EC,再证明△EHB≌△PHG(SAS),推出△EHP是等腰直角三角形即可解决问题.
(1)解:如图1中,
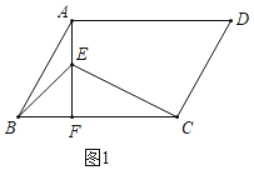
∵AF⊥BC,
∴∠AFB=∠CFE=90°,
∵∠EBC=45°,
∴∠EBF=∠BEF=45°,
∴FB=FE,
∵∠BAF=∠ECF,
∴△AFB≌△CFE(AAS),
∴BF=EF=1,
∵AB=![]() ,
,
∴AF=CF=![]() =2,
=2,
∴BC=BF+CF=3,
∵四边形ABCD是平行四边形,
∴AD=BC=3;
(2)证明:如图2中,设PG交BE于T,BE交GH于Q.
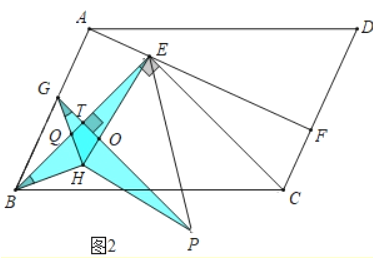
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AF⊥CD,
∴AF⊥AB,
∴∠BAE=∠EFC=90°,
∵∠BEC=90°,
∴∠AEB+∠CEF=90°,∠CEF+∠ECF=90°,
∴∠AEB=∠ECF,
∵AE=CF,
∴△BAE≌△EFC(ASA),
∴BE=EC,
∵GP=EC,
∴GP=BE,
∵GP⊥BE,
∴∠GTQ=90°,
∵BH=GH,∠BHG=90°,
∴∠BHQ=∠GTQ,
∵∠GQT=∠BQH,
∴∠HGP=∠HBE,
∴△EHB≌△PHG(SAS),
∴EH=PH,∠TEO=∠OPH,
∵∠EOT=∠POH,
∴∠PHO=∠ETO=90°,
∴△EHP是等腰直角三角形,
∴PE=![]() EH.
EH.
故答案为:(1)AD=3.(2)见解析.


科目:初中数学 来源: 题型:
【题目】如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距______千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
(3)B出发后______小时与A相遇.
(4)若B的自行车不发生故障,保持出发时的速度前进,______小时与A相遇,相遇点离B的出发点______千米.在图中表示出这个相遇点C.
(5)求出A行走的路程S与时间t的函数关系式。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考英语听力测试期间,需要杜绝考点周围的噪音![]() 如图,点A是我市一中考点,在位于A考点南偏西
如图,点A是我市一中考点,在位于A考点南偏西![]() 方向距离120米的C点处有一消防队
方向距离120米的C点处有一消防队![]() 在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东
在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东![]() 方向的F点处突发火灾,消防队必须立即赶往救火
方向的F点处突发火灾,消防队必须立即赶往救火![]() 已知消防车的警报声传播半径为110米,问消防车的警报声对听力测试是否会造成影响?若会造成影响,已知消防车行驶的速度为每小时60千米,则对听力测试的影响时间为几秒?
已知消防车的警报声传播半径为110米,问消防车的警报声对听力测试是否会造成影响?若会造成影响,已知消防车行驶的速度为每小时60千米,则对听力测试的影响时间为几秒?![]() ,结果精确到1秒
,结果精确到1秒![]()
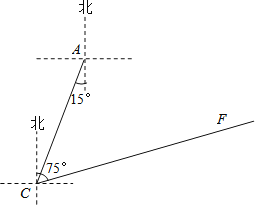
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌网上旗舰店售卖两种规格的积木玩具:A规格一盒里面一个独立包装袋,共有40块积木;B规格一盒里面有三个独立包装袋,共有n块积木.小开的爸爸在网上买了两种规格的积木若干盒,结果运输过程中遭遇暴力快递,收货时发现里面的独立包装袋被损坏,积木全部混在了一起,经盘点发现,共有20个独立包装袋和290块积木,则n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在某一次实验中,测得两个变量之间的关系如下表所示:
自变量x | 1 | 2 | 3 | 4 | 12 | |
因变量y | 12.03 | 5.98 | 3.04 | 1.99 | 1.00 |
请你根据表格回答下列问题:
① 这两个变量之间可能是怎样的函数关系?你是怎样作出判断的?请你简要说明理由。
②请你写出这个函数的解析式。
③表格中空缺的数值可能是多少?请你给出合理的数值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司要将本公司100吨货物运往某地销售,经与运输公司协商,计划租用甲、乙两种型号的汽车共6辆,用这6辆汽车次将货物全部运走,其中每辆甲型汽车最多能装该种货物16吨,每辆乙型汽车最多能装该种货物18吨,已知租用1辆甲型汽车和2辆乙型汽车共需费用2600元;租用2辆甲型汽车和1辆乙型汽车共需费用2500元,且同一型号汽车每辆租车费用相同.
(1)求租用辆甲型汽车、一辆乙型汽车的费用分别是多少元?
(2)若这个公司计划此次租车费用不超过5200元,通过计算求出该公司有几种租车方案?请你设计出来,并求出最低的租车费用,
查看答案和解析>>
科目:初中数学 来源: 题型:
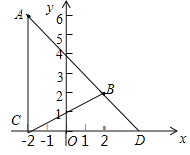
【题目】在平面直角坐标系中,已知A(a,b),B(2,2),且|a-b+8|+![]() =0.
=0.
(1)求点A的坐标;
(2)过点A作AC⊥x轴于点C,连接BC,AB,延长AB交x轴于点D,设AB交y轴于点E,那么OD与OE是否相等?请说明理由.
(3)在x轴上是否存在点P,使S△OBP=S△BCD?若存在,请求出P点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李晖到“宇泉牌”服装专卖店做社会调查.了解到商店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员 | 小俐 | 小花 |
月销售件数(件) | 200 | 150 |
月总收入(元) | 1400 | 1250 |
假设月销售件数为![]() 件,月总收入为
件,月总收入为![]() 元,销售每件奖励
元,销售每件奖励![]() 元,营业员月基本工资为
元,营业员月基本工资为![]() 元.
元.
(1)求![]() 的值;
的值;
(2)若营业员小俐某月总收入不低于![]() 元,那么小俐当月至少要卖服装多少件?
元,那么小俐当月至少要卖服装多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com