
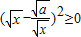 ,所以x-
,所以x-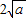 +
+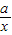 ≥0,从而x+
≥0,从而x+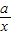 ≥
≥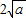 (当x=
(当x=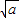 )是取等号).
)是取等号).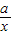 (a>0,x>0).由上述结论可知:当x=
(a>0,x>0).由上述结论可知:当x=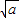 时,该函数有最小值为2
时,该函数有最小值为2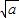 .
.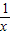 (x>0),则当x=______时,y1+y2取得最小值为______.
(x>0),则当x=______时,y1+y2取得最小值为______.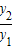 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.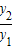 的表达式,然后将(x+1)看做一个整体,继而再运用所给结论即可.
的表达式,然后将(x+1)看做一个整体,继而再运用所给结论即可.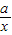 (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x=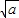 时,该函数有最小值为2
时,该函数有最小值为2 .
.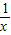 (x>0),则当x=1时,y1+y2取得最小值为2.
(x>0),则当x=1时,y1+y2取得最小值为2.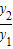 =
=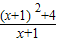 =(x+1)+
=(x+1)+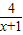 的最小值为:2
的最小值为:2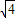 =4,
=4,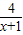 =4时,
=4时,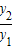 的最小值为4,相应的x的值为1;
的最小值为4,相应的x的值为1;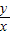 =0.001x+
=0.001x+ +1.6=0.001x+
+1.6=0.001x+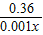 +1.6,
+1.6,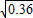 时,
时,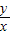 取得最小,此时x=600km,
取得最小,此时x=600km,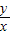 ≥2
≥2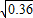 +1.6=2.8,
+1.6=2.8,

 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
| x |
| ||
|
| a |
| a |
| x |
| a |
| x |
| a |
| a |
| a |
| x |
| a |
| a |
| 1 |
| x |
| y2 |
| y1 |
查看答案和解析>>
科目:初中数学 来源:盐城 题型:解答题
| x |
| ||
|
| a |
| a |
| x |
| a |
| x |
| a |
| a |
| a |
| x |
| a |
| a |
| 1 |
| x |
| y2 |
| y1 |
查看答案和解析>>
科目:初中数学 来源:2013年5月中考数学模拟试卷(38)(解析版) 题型:解答题
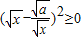 ,所以x-
,所以x-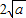 +
+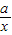 ≥0,从而x+
≥0,从而x+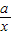 ≥
≥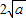 (当x=
(当x=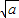 )是取等号).
)是取等号).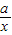 (a>0,x>0).由上述结论可知:当x=
(a>0,x>0).由上述结论可知:当x=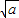 时,该函数有最小值为2
时,该函数有最小值为2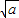 .
.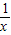 (x>0),则当x=______时,y1+y2取得最小值为______.
(x>0),则当x=______时,y1+y2取得最小值为______.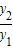 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.查看答案和解析>>
科目:初中数学 来源:2012年江苏省盐城市中考数学试卷(解析版) 题型:解答题
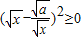 ,所以x-
,所以x- +
+ ≥0,从而x+
≥0,从而x+ ≥
≥ (当x=
(当x= )是取等号).
)是取等号). (a>0,x>0).由上述结论可知:当x=
(a>0,x>0).由上述结论可知:当x= 时,该函数有最小值为2
时,该函数有最小值为2 .
. (x>0),则当x=______时,y1+y2取得最小值为______.
(x>0),则当x=______时,y1+y2取得最小值为______. 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com