
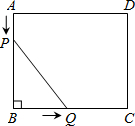
 �ھ���ABCD�У���֪AB=5cm��BC=6cm����P�ӵ�A��ʼ�ر�AB���յ�B��1cm/s���ٶ��˶���ͬʱ����Q�ӵ�B��ʼ�ر�BC���յ�C��2cm/s���ٶ��˶�������Q�˶�����Cʱ������ֹͣ�˶������˶�ʱ��Ϊt�룮
�ھ���ABCD�У���֪AB=5cm��BC=6cm����P�ӵ�A��ʼ�ر�AB���յ�B��1cm/s���ٶ��˶���ͬʱ����Q�ӵ�B��ʼ�ر�BC���յ�C��2cm/s���ٶ��˶�������Q�˶�����Cʱ������ֹͣ�˶������˶�ʱ��Ϊt�룮���� ��1�����ݵ�P�͵�Q�˶����ٶȺ�ʱ������AP��BQ�ij���Ȼ������PB=AB-PA�����PB�ij���
��2��Rt��PBQ�У����ݹ��ɶ����ɵõ�����t�ķ��̣��Ӷ������t��ֵ��
��3������þ���ABCD�������Ȼ��������ε��������á�PQB�����=4cm2��Ȼ�����ݡ�PQB�����=4cm2�г�����t�ķ��̣��Ӷ������t��ֵ��
��� �⣺��1����P�ӵ�A��ʼ�ر�AB���յ�B��1cm/s���ٶ��ƶ���
��AP=tcm��
��AB=5cm��
��PB=��5-t��cm��
�ߵ�Q�ӵ�B��ʼ�ر�BC���յ�C��2cm/s���ٶ��ƶ���
��BQ=2tcm��
��2����Rt��PBQ�У����ݹ��ɶ�����֪��PB2+BQ2=PQ2��������5-t��2+��2t��2=52��
��ã�t1=0������������ȥ����t2=2
��t=2��ʱ��PQ�ij��ȵ���5cm��
��3������t=1�룬ʹ�������APQCD���������26cm2��
�������£�������ABCD������ǣ�5��6=30��cm2��
ʹ�������APQCD���������26cm2
���PBQ�����Ϊ30-26=4��cm2��
��$\frac{1}{2}$����5-t����2t=4��
��ã�t1=4������������ȥ����t2=1��
����t=1��ʱ��ʹ�������APQCD���������26cm2��
���� ������Ҫ��������ı��ε��ۺ�Ӧ�ã��������ҪӦ���˾��ε����ʡ����ɶ����������ε������ʽ�����ݹ��ɶ����������ε������ʽ�г�����t�ķ����ǽ���Ĺؼ���


 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��AOB�У�OA=OB=3$\sqrt{2}$����O�İ뾶Ϊ$\sqrt{2}$����P��AB���ϵ�һ���㣬����P����O��һ������PQ����QΪ�е㣩����PQ���ȵ�ȡֵ��ΧΪ$\sqrt{7}$��PQ��4��
��ͼ����Rt��AOB�У�OA=OB=3$\sqrt{2}$����O�İ뾶Ϊ$\sqrt{2}$����P��AB���ϵ�һ���㣬����P����O��һ������PQ����QΪ�е㣩����PQ���ȵ�ȡֵ��ΧΪ$\sqrt{7}$��PQ��4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AC=6��BD=8��������ABCD�ĸ�AH��ֵ�ǣ�������
��ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AC=6��BD=8��������ABCD�ĸ�AH��ֵ�ǣ�������| A�� | 4 | B�� | 5 | C�� | $\frac{24}{5}$ | D�� | $\frac{48}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У���D��E�ֱ��ڱ�AB��AC�ϣ���ADE=��C����BAC��ƽ����AG�ֱ��߶�DE��BC�ڵ�F��G��
��ͼ����ABC�У���D��E�ֱ��ڱ�AB��AC�ϣ���ADE=��C����BAC��ƽ����AG�ֱ��߶�DE��BC�ڵ�F��G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com