
”¾ĢāÄæ”æŅŃÖŖČĪŅāČż½ĒŠĪµÄČż±ß³¤£¬ČēŗĪĒóČż½ĒŠĪĆ껿£æ
¹ÅĻ£Ą°µÄ¼øŗĪѧ¼Ņŗ£Ā×½ā¾öĮĖÕāøöĪŹĢā£¬ŌŚĖūµÄÖų×÷”¶¶ČĮæĀŪ”·Ņ»ŹéÖŠøų³öĮĖ¼ĘĖć¹«Ź½©©ŗ£Ā×¹«Ź½S=![]() £ØĘäÖŠa£¬b£¬cŹĒČż½ĒŠĪµÄČż±ß³¤£¬p=
£ØĘäÖŠa£¬b£¬cŹĒČż½ĒŠĪµÄČż±ß³¤£¬p=![]() £¬SĪŖČż½ĒŠĪµÄĆ껿£©£¬²¢øų³öĮĖÖ¤Ć÷
£¬SĪŖČż½ĒŠĪµÄĆ껿£©£¬²¢øų³öĮĖÖ¤Ć÷
ĄżČē£ŗŌŚ”÷ABCÖŠ£¬a=3£¬b=4£¬c=5£¬ÄĒĆ“ĖüµÄĆ껿æÉŅŌÕāŃł¼ĘĖć£ŗ
”ßa=3£¬b=4£¬c=5
”ąp=![]() =6
=6
”ąS=![]() =
=![]() =6
=6
ŹĀŹµÉĻ£¬¶ŌÓŚŅŃÖŖČż½ĒŠĪµÄČż±ß³¤ĒóČż½ĒŠĪĆ껿µÄĪŹĢā£¬»¹æÉÓĆĪŅ¹śÄĻĖĪŹ±ĘŚŹżŃ§¼ŅĒŲ¾ÅÉŲĢį³öµÄĒŲ¾ÅÉŲ¹«Ź½µČ·½·Ø½ā¾ö£®
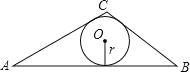
ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬BC=5£¬AC=6£¬AB=9
£Ø1£©ÓĆŗ£Ā×¹«Ź½Ēó”÷ABCµÄĆ껿£»
£Ø2£©Ēó”÷ABCµÄÄŚĒŠŌ²°ė¾¶r£®
”¾“š°ø”æ£Ø1£©10![]() £»£Ø2£©r=
£»£Ø2£©r=![]() £®
£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©ĻČøł¾ŻBC”¢AC”¢ABµÄ³¤Ēó³öP£¬ŌŁ“śČėµ½¹«Ź½S=![]() ¼“æÉĒóµĆSµÄÖµ£»£Ø2£©øł¾Ż¹«Ź½S=
¼“æÉĒóµĆSµÄÖµ£»£Ø2£©øł¾Ż¹«Ź½S=![]() r£ØAC+BC+AB£©£¬“śČėæÉµĆ¹ŲÓŚrµÄ·½³Ģ£¬½ā·½³ĢµĆrµÄÖµ£®
r£ØAC+BC+AB£©£¬“śČėæÉµĆ¹ŲÓŚrµÄ·½³Ģ£¬½ā·½³ĢµĆrµÄÖµ£®
ŹŌĢā½āĪö£ŗ£Ø1£©”ßBC=5£¬AC=6£¬AB=9£¬
”ąp=![]() =
=![]() =10£¬
=10£¬
”ąS=![]() =
=![]() =10
=10![]() £»
£»
¹Ź”÷ABCµÄĆ껿10![]() £»
£»
£Ø2£©”ßS=![]() r£ØAC+BC+AB£©£¬
r£ØAC+BC+AB£©£¬
”ą10![]() =
=![]() r£Ø5+6+9£©£¬
r£Ø5+6+9£©£¬
½āµĆ£ŗr=![]() £¬
£¬
¹Ź”÷ABCµÄÄŚĒŠŌ²°ė¾¶r=![]() £®
£®


 ĆæČÕ10·ÖÖÓæŚĖćŠÄĖćĖŁĖćĢģĢģĮ·ĻµĮŠ“š°ø
ĆæČÕ10·ÖÖÓæŚĖćŠÄĖćĖŁĖćĢģĢģĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČż½ĒŠĪĮ½±ßµÄ³¤ŹĒ6ŗĶ8£¬µŚČż±ßĀś×ć·½³Ģx2©24x+140£½0£¬ŌņČż½ĒŠĪÖܳ¤ĪŖ£Ø””””£©
A.24B.28C.24»ņ28D.ŅŌÉĻ¶¼²»¶Ō
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠŠŌÖŹÖŠ£¬ĮāŠĪ¶Ō½ĒĻß²»¾ßÓŠµÄŹĒ£Ø £©
A.¶Ō½ĒĻß»„Ļą“¹Ö±
B.¶Ō½ĒĻßĖłŌŚÖ±ĻߏĒ¶Ō³ĘÖį
C.¶Ō½ĒĻßĻąµČ
D.¶Ō½ĒĻß»„ĻąĘ½·Ö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
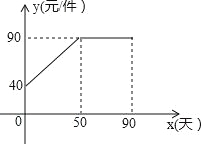
”¾ĢāÄæ”æ¾ÅÄź¼¶£Ø3£©°ąŹżŃ§ŠĖȤŠ”×é¾¹żŹŠ³”µ÷²éÕūĄķ³öijÖÖÉĢĘ·ŌŚµŚxĢģ£Ø1”Üx”Ü90£¬ĒŅxĪŖÕūŹż£©µÄŹŪ¼ŪÓėĻśŹŪĮæµÄĻą¹ŲŠÅĻ¢ČēĻĀ£®ŅŃÖŖÉĢĘ·µÄ½ų¼ŪĪŖ30ŌŖ/¼ž£¬ÉčøĆÉĢĘ·µÄŹŪ¼ŪĪŖy£Øµ„Ī»£ŗŌŖ/¼ž£©£¬ĆæĢģµÄĻśŹŪĮæĪŖp£Øµ„Ī»£ŗ¼ž£©£¬ĆæĢģµÄĻśŹŪĄūČóĪŖw£Øµ„Ī»£ŗŌŖ£©£®
Ź±¼äx£ØĢģ£© | 1 | 30 | 60 | 90 |
ĆæĢģĻśŹŪĮæp£Ø¼ž£© | 198 | 140 | 80 | 20 |
£Ø1£©Ēó³öwÓėxµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©ĪŹĻśŹŪøĆÉĢĘ·µŚ¼øĢģŹ±£¬µ±ĢģµÄĻśŹŪĄūČó×ī“ó£æ²¢Ēó³ö×ī“óĄūČó£»
£Ø3£©øĆÉĢĘ·ŌŚĻśŹŪ¹ż³ĢÖŠ£¬¹²ÓŠ¶ąÉŁĢģĆæĢģµÄĻśŹŪĄūČó²»µĶÓŚ5600ŌŖ£æĒėÖ±½ÓŠ“³ö½į¹ū£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČō¹ŲÓŚxµÄ·½³Ģ3£Øx©1£©+a=b£Øx+1£©ŹĒŅ»ŌŖŅ»“Ī·½³Ģ£¬Ōņ£Ø””””£©
A. a£¬bĪŖČĪŅāÓŠĄķŹż B. a”Ł0
C. b”Ł0 D. b”Ł3
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øöĮ½Ī»ŹżŹĒa£¬»¹ÓŠŅ»øöČżĪ»ŹżŹĒb£¬Čē¹ū°ŃÕāøöĮ½Ī»Źż·ÅŌŚÕāøöČżĪ»ŹżµÄĒ°Ćę£¬×é³ÉŅ»øöĪåĪ»Źż£¬ŌņÕāøöĪåĪ»ŹżµÄ±ķŹ¾·½·ØŹĒ£Ø””””£©
A. 10a+b B. 100a+b C. 1000a+b D. a+b
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
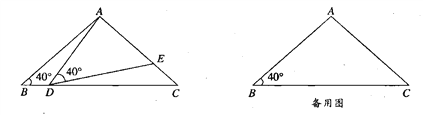
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB£½AC£½4£¬”ĻB£½40”ć£¬µćDŌŚĻ߶ĪBCÉĻŌĖ¶Æ(D²»ÓėB”¢CÖŲŗĻ)£¬Į¬½ÓAD£¬×÷”ĻADE£½40”ć£¬DE½»Ļ߶ĪACÓŚE£®
(1)µ±”ĻBDA£½115”揱£¬”ĻEDC£½ ”ć£¬”ĻDEC£½ ”ć£»
(2)ŌŚµćDµÄŌĖ¶Æ¹ż³ĢÖŠ£¬”÷ADEµÄŠĪדæÉŅŌŹĒµČŃüČż½ĒŠĪĀš£æČōæÉŅŌ£¬Ēó³ö”ĻBDAµÄ¶ČŹż£®Čō²»æÉŅŌ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij¹ĖæĶŅŌ°ĖÕŪµÄÓÅ»Ż¼ŪĀņĮĖŅ»¼žÉĢĘ·£¬±Č±ź¼ŪÉŁø¶ĮĖ30ŌŖ£¬ÄĒĆ“Ėū¹ŗĀņÕā¼žÉĢĘ·»ØĮĖŌŖ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø1£©ČēĶ¼1£¬”ĻMAN=90”ć£¬ÉäĻßAEŌŚÕāøö½ĒµÄÄŚ²æ£¬µćB”¢C·Ö±šŌŚ”ĻMANµÄ±ßAM”¢ANÉĻ£¬ĒŅAB=AC£¬CF”ĶAEÓŚµćF£¬BD”ĶAEÓŚµćD£®ĒóÖ¤£ŗ”÷ABD”Õ”÷CAF£»
£Ø2£©ČēĶ¼2£¬µćB”¢C·Ö±šŌŚ”ĻMANµÄ±ßAM”¢ANÉĻ£¬µćE”¢F¶¼ŌŚ”ĻMANÄŚ²æµÄÉäĻßADÉĻ£¬”Ļ1”¢”Ļ2·Ö±šŹĒ”÷ABE”¢”÷CAFµÄĶā½Ē£®ŅŃÖŖAB=AC£¬ĒŅ”Ļ1=”Ļ2=”ĻBAC£®ĒóÖ¤£ŗ”÷ABE”Õ”÷CAF£»
£Ø3£©ČēĶ¼3£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬AB£¾BC£®µćDŌŚ±ßBCÉĻ£¬CD=2BD£¬µćE”¢FŌŚĻ߶ĪADÉĻ£¬”Ļ1=”Ļ2=”ĻBAC£®Čō”÷ABCµÄĆ껿ĪŖ15£¬Ēó”÷ACFÓė”÷BDEµÄĆ껿֮ŗĶ£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com