【答案】
分析:(1)应先判断出和∠E组成的三角形的其余两个角的度数之和,再根据三角形内角和定理即可求出∠AEB的度数;
(2)根据平行得到同旁内角的关系,以及角平分线的定义推出和∠E组成的三角形的其余两个角的度数之和;
(3)应从点D和点C的不同位置入手,分情况进行讨论.
解答: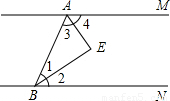
(1)解:90°;
(2)证明:如图,
∵AE、BE分别平分∠NBA、∠MAB,
∴∠1=∠2,∠3=∠4,
又∵AM∥BN,
∴∠MAB+∠NBA=180°,
即∠1+∠2+∠3+∠4=180°,
∠1+∠1+∠3+∠3=180°,
∴2(∠1+∠3)=180°,
∠1+∠3=90°,
从而∠AEB=180°-(∠1+∠3)=90°;
(3)解:①当点D在射线AM的反向延长线上、点C在射线BN上时(如图),
线段AD、BC、AB三者间的关系为:
BC=AB+AD.
证法一:延长AE交BN于点F.
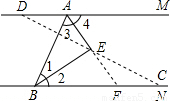
∵AM∥BN,
∴∠4=∠AFB,
又∠3=∠4,
∴∠AFB=∠3,
∴BF=BA(等角对等边),
即△BAF为等腰三角形.
由(1)∠AEB=90°知BE⊥AF,
即BE为等腰△BAF底边AF上的高,
由“三线合一”定理,得AE=EF.
由AM∥BN得∠ADE=∠FCE,
又∠AED=∠FEC,
∴△ADE≌△FCE,
∴AD=FC,
BC=BF+FC及BF=AB、FC=AD
得BC=AB+AD
(特殊情况:点D与A点重合时,C点即是上图的F点,
AD=0,BC=BF,由上述证明过程知,仍有BC=AB+AD);
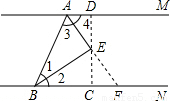
②当点D在射线AM上,点C在射线BN上时(如图),
线段AD、BC、AB三者间的关系为:AB=AD+BC.
证明如下:
由①的证明可知,若延长AE交BN于点F,则AE=EF,
即E为AF的中点,易证△AED≌△FEC,
∴AD=CF,
由①知,△ABF为等腰三角形,AB=BF=BC+CF,
即AB=AD+BC;
③当点D在射线AM上,点C在射线BN的反向延长线上时(如图),
线段AD、BC、AB三者间的关系为:
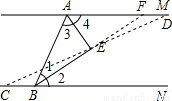
AD=AB+BC.
证明如下:延长BE交AM于点F,
∵AM∥BN,
∴∠2=∠AFB,
又∵∠1=∠2,
∴∠1=∠AFB,
∴AF=AB.
∵∠AEB=90°,即AE为等腰△ABF底边BF上的高,
∴BE=FE(“三线合一”定理),易证△EBC≌△EFD,
∴BC=FD.
从而AD=AF+FD=AB+BC.
(特殊情况:当点C与点B重合时,由上述证明过程知,上式也成立)
点评:本题考查了三角形全等的判定及性质;本题需注意多种情况的分析,利用全等来得到各线段之间的等量关系.

 (1)解:90°;
(1)解:90°;




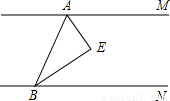
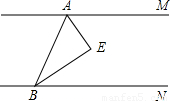
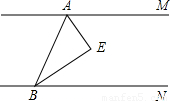
 24、如图,直线AM∥BN,AE、BE分别平分∠MAB、∠NBA.
24、如图,直线AM∥BN,AE、BE分别平分∠MAB、∠NBA. 如图,直线AM∥BN,AE、BE分别平分∠MAB、∠NBA.
如图,直线AM∥BN,AE、BE分别平分∠MAB、∠NBA.