
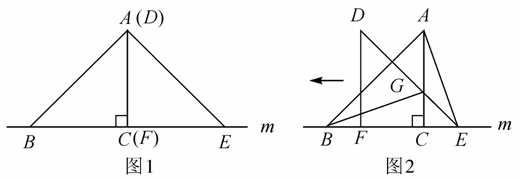
如图,△ABC的边BC在直线m上,AC⊥BC,且AC=BC,△DEF的边FE也在直线m上,边DF与边AC重合,且DF=EF.
(1)在图1中,请你通过观察、思考,猜想并写出AB与AE所满足的数量关系和位置关系;(不要求证明)
(2)将△DEF沿直线m向左平移到图2的位置时,DE交AC于点G,连接AE、BG.猜想△BCG与△ACE能否通过旋转重合?请证明你的猜想.
解 (1)AB=AE,AB⊥AE. …………………4分
(2)将△BCG绕点C顺时针旋转90°后能与△ACE重合:………………5分
(或将△ACE绕点C逆时针旋转90°后能与△BCG重合),理由如下
∵AC⊥BC,DF⊥EF,B、F、C、E共线,
∴∠ACB=∠ACE=∠DFE=90°.
又∵AC=BC,DF=EF,∴∠DEF=∠D=45°. ……………8分
在△CEG中,∵∠ACE=90°,
∴∠CGE=∠DEF=45°,
∴CG=CE. ……………………………10分
在△BCG和△ACE中,
∵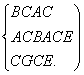
∴△BCG≌△ACE(SAS)![]() .……………………13分
.……………………13分
∴将△BCG绕点C顺时针旋转90°后能与△ACE重合(或将△ACE绕点C逆![]() 时针旋转90°后能与△BCG重合).………………14分
时针旋转90°后能与△BCG重合).………………14分


科目:初中数学 来源: 题型:
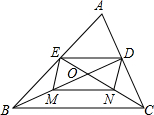 如图,△ABC的边AC、AB上的中线BD、CE相交于点O,M、N分别是BO、CO的中点,顺次连接点D、E、M、N.
如图,△ABC的边AC、AB上的中线BD、CE相交于点O,M、N分别是BO、CO的中点,顺次连接点D、E、M、N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com