
【题目】(10分)某班“数学兴趣小组”对函数![]() 的图像和性质进行了探究,探究过程如下,请补充完整.
的图像和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … |
|
|
|
| 0 | 1 | 2 | 3 | 4 | … |
| … | 3 |
|
|
| 0 |
| 0 |
| 3 | … |
其中,![]() =____________.
=____________.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图像的一部分,请画出该图像的另一部分.
(3)观察函数图像,写出两条函数的性质:

(4)进一步探究函数图像发现:
①函数图像与![]() 轴有__________个交点,所以对应方程
轴有__________个交点,所以对应方程![]() 有___________个实数根;
有___________个实数根;
②方程![]() 有___________个实数根;
有___________个实数根;
③关于![]() 的方程
的方程![]() 有4个实数根,
有4个实数根,![]() 的取值范围是_______________________
的取值范围是_______________________
【答案】(1)0;(2)图见解析;(3)答案不唯一,合理即可;(4)①3,3;②2;③-1<a<0.
【解析】
试题分析:(1)观察表格,根据对称性即可得m=0;(2)根据表格描点,画出图象即可;(3)观察图象,写出函数的两条性质即可,可从函数的最值,增减性,图象的对称性等方面阐述,答案不唯一,合理即可;(4)①观察函数图像可得函数图像与![]() 轴有3个交点,所以对应方程
轴有3个交点,所以对应方程![]() 有3个实数根;②由图象可知,函数
有3个实数根;②由图象可知,函数![]() 图像与直线y=2有两个交点,所以方程有2个实数根;③方程
图像与直线y=2有两个交点,所以方程有2个实数根;③方程![]() 有4个实数根,说明函数
有4个实数根,说明函数![]() 的图象与直线y=a有4个交点,由此可得
的图象与直线y=a有4个交点,由此可得![]() 的取值范围是-1<a<0.
的取值范围是-1<a<0.
试题解析:(1)0;
(2)(正确补全图象);

(3)(可从函数的最值,增减性,图象的对称性等方面阐述,答案不唯一,合理即可);
(4)①3,3;②2;③-1<a<0.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,BC是⊙O的切线,B为切点,OC平行于弦AD,连接CD。过点D作DE⊥AB于E,交AC于点P,求证:点P平分线段DE。

查看答案和解析>>
科目:初中数学 来源: 题型:
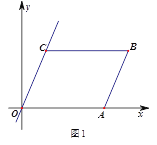
【题目】如图,在平面直角坐标系中,四边形OABC是平行四边形.直线L经过O、C两点.点A的坐标为(8,0),点B的坐标为(11,4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C﹣B相交于点M.当Q、M两点相遇时,P、Q两点停止运动,设点P、Q运动的时间为t秒(t>0).△MPQ的面积为S.
(1)点C的坐标为 ,直线L的解析式为 .
(2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围.
(3)试求题(2)中当t为何值时,S的值最大,并求出S的最大值.
(4)随着P、Q两点的运动,当点M在线段CB上运动时,设PM的延长线与直线L相交于点N.试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两个全等的直角三角形拼下列图形:①平行四边形(不包含菱形、矩形、正方形);②矩形;③菱形;④正方形;⑤等腰三角形.一定可以拼成的图形是_____________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题: 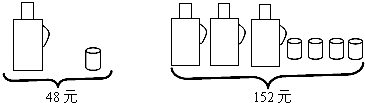
(1)一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和20个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪和小敏在研究绝对值的问题时,遇到了这样一道题:
(1)当式子|x﹣1|+|x+5|取最小值时,x应满足的条件是 , 此时的最小值是 . 小聪说:利用数轴求线段的长可以解决这个问题.如图,点A,B对应的数分别为﹣5,1,则线段AB的长为6,我发现也可通过|1﹣(﹣5)|或|﹣5﹣1|来求线段AB的长,即数轴上两点间的线段的长等于它们所对应的两数差的绝对值.![]()
小敏说:我明白了,若点C在数轴上对应的数为x,线段AC的长就可表示为|x﹣(﹣5)|,那么|x﹣1|表示的是线段的长.
小聪说:对,求式子|x﹣1|+|x+5|的最小值就转化为数轴上求线段AC+BC长的最小值,而点C在线段AB上时AC+BC=AB最小,最小值为6.
小敏说:点C在线段AB上,即x取﹣5,1之间的有理数(包括﹣5,1),因此相应x的取值范围可表示为﹣5≤x≤1时,最小值为6.
请你根据他们的方法解决下面的问题:
(2)小敏说的|x﹣1|表示的是线段的长;
(3)当式子|x﹣3|+|x+2|取最小值时,x应满足的条件是;
(4)当式子|x﹣2|+|x+3|+|x+4|取最小值时,x应满足的条件是;
(5)当式子|x﹣a|+|x﹣b|+|x﹣c|+|x﹣d|(a<b<c<d)取最小值时,x应满足的条件是 , 此时的最小值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com