
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 的弦,
的弦,![]() ,
,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 于点
于点![]() .
.
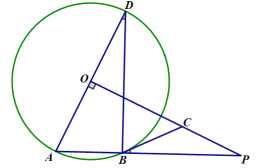
(1)求证:![]() ;
;
(2)若![]() ,求线段
,求线段![]() 的长.
的长.
科目:初中数学 来源: 题型:
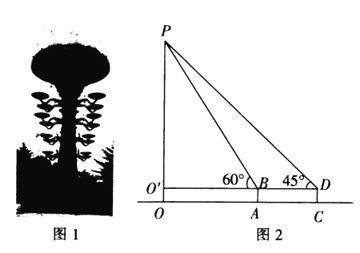
【题目】如图1所示的是宝鸡市文化景观标志“天下第一灯”,它由国际![]() 不锈钢板整体锻造,表面涂有仿古金色漆,以仿青铜纹饰雕刻的柱体四盏灯分
不锈钢板整体锻造,表面涂有仿古金色漆,以仿青铜纹饰雕刻的柱体四盏灯分![]() 层布置.一天上午,数学兴趣小组的同学们带着测量工具来测量“天下第一灯”的高度,由于有围栏保护,他们无法到达灯的底部
层布置.一天上午,数学兴趣小组的同学们带着测量工具来测量“天下第一灯”的高度,由于有围栏保护,他们无法到达灯的底部![]() 他们制定了一种测量方案,图2所示的是他们测量方案的示意图,先在周围的广场上选择一点
他们制定了一种测量方案,图2所示的是他们测量方案的示意图,先在周围的广场上选择一点![]() 并在点
并在点![]() 处安装了测量器
处安装了测量器![]() 在点
在点![]() 处测得该灯的顶点P的仰角为
处测得该灯的顶点P的仰角为![]() ;再在
;再在![]() 的延长线上确定一点
的延长线上确定一点![]() 使
使![]() 米,在
米,在![]() 点处测得该灯的顶点
点处测得该灯的顶点![]() 的仰角为
的仰角为![]() .若测量过程中测量器的高度始终为
.若测量过程中测量器的高度始终为![]() 米,求“天下第一灯”的高度.
米,求“天下第一灯”的高度.![]() ,最后结果取整数)
,最后结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,⊙O分别切AB于M,BC于N,连接BO、CO,BO=CO.

(1)求证:AC是⊙O的切线;
(2)连接MC,若![]() ,求sin∠B的值.
,求sin∠B的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
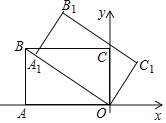
【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2![]() ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象过点A(1,2),B(3,2),C(5,7).若点M(﹣2,y1),N(﹣1,y2),K(8,y3)也在二次函数y=ax2+bx+c的图象上,则y1,y2,y3从小到大的关系是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,现给出以下四个结论:(1)AE=CF;(2)△EPF是等腰直角三角形;(3)S四边形AEPF=![]() S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )
S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )

A.1个B.3个C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
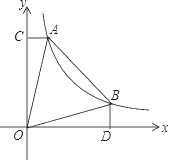
【题目】如图,A、B两点在反比例函数![]() (k>0,x>0)的图象上,AC⊥y轴于点C,BD⊥x轴于点D,点A的横坐标为a,点B的横坐标为b,且a<b.
(k>0,x>0)的图象上,AC⊥y轴于点C,BD⊥x轴于点D,点A的横坐标为a,点B的横坐标为b,且a<b.
(1)若△AOC的面积为4,求k值;
(2)若a=1,b=k,当AO=AB时,试说明△AOB是等边三角形;
(3)若OA=OB,证明:OC=OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平行四边形ABCD中,AE⊥BC,垂足为E,CE=AB,点F为CE的中点,点G在线段CD上,联结DF,交AG于点M,交EG于点N,且∠DFC=∠EGC.
(1)求证:CG=DG;
(2)求证:![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com