

���� ��1����ͼ1�У���DH��BC��H�����ı���ABHD�Ǿ��Σ����ȱ������Ρ�EGF�ĸ�=$\sqrt{3}$ʱ����G��AD�ϣ���ʱx=2������F��C�غ�ʱ��BE=$\frac{1}{2}$BC=3����ʱx=3��
��2�����������Σ��ٵ�CF=CD��F��C���ʱ����CF=CD��F��C�Ҳ�ʱ����FC=DFʱ���ֱ����̼��ɽ�����⣻
��3����ͼ1��ͼ2��ͼ3�������ν�����⣮�ٵ�0��x��2ʱ����ͼ1�У���EFG���ı���ABCD�ڲ����ص����־��ǡ�EFG��
�ڵ�2��x��3ʱ����ͼ2�У���E��F���߶�BC�ϣ���EFG���ı���ABCD�ص�����Ϊ�ı���EFNM��
�۵�3��x��6ʱ����ͼ3�У���E���߶�BC�ϣ���F������BC�ϣ��ص������ǡ�ECP��
��� �⣺��1����ͼ1�У���DH��BC��H�����ı���ABHD�Ǿ��Σ�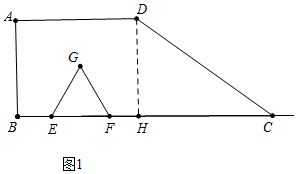
��AD=BH=3��BC=6��
��CH=BC-BH=3��
��Rt��DHC�У�CH=3����DCH=30�㣬
��DH=CH•tan30��=$\sqrt{3}$��
���ȱ������Ρ�EGF�ĸ�=$\sqrt{3}$ʱ����G��AD�ϣ���ʱx=2��
����F��C�غ�ʱ��BE=$\frac{1}{2}$BC=3����ʱx=3��
���Ե�G���ı���ABCD�ı���ʱ��x=2����F���C�غ�ʱ��x=3��
�ʴ�Ϊ2��3��
��2��ע�0��x��6���ʡ�DFCΪ����������ֻ���������Σ�
�ٵ�CF=CD��F��C���ʱ��6-2x=2$\sqrt{3}$��x=3-$\sqrt{3}$��
�ڵ�CF=CD��F��C�Ҳ�ʱ��2x-6=2$\sqrt{3}$��x=3+$\sqrt{3}$��
�۵�FC=DFʱ��6-2x=$\sqrt{3}$��x=$\frac{6-\sqrt{3}}{2}$��
����������x��ֵΪ3-$\sqrt{3}$��3+$\sqrt{3}$��$\frac{6-\sqrt{3}}{2}$��
��3���ٵ�0��x��2ʱ����ͼ1�У���EFG���ı���ABCD�ڲ�������y=$\frac{\sqrt{3}}{4}$x2��
�ڵ�2��x��3ʱ����ͼ2�У���E��F���߶�BC�ϣ���EFG���ı���ABCD�ص�����Ϊ�ı���EFNM��
�ߡ�FNC=��FCN=30�㣬
��FN=FC=6-2x��
��GN=3x-6��
�ߡ�G=60�㣬
���GNM��ֱ�������Σ�
��y=S��EFG-S��GMN=$\frac{\sqrt{3}}{4}$x2-$\frac{\sqrt{3}}{8}$��3x-6��2=-$\frac{7\sqrt{3}}{8}$x2+$\frac{9\sqrt{3}}{2}$x-$\frac{9\sqrt{3}}{2}$��
�۵�3��x��6ʱ����ͼ3�У���E���߶�BC�ϣ���F������BC�ϣ��ص������ǡ�ECP��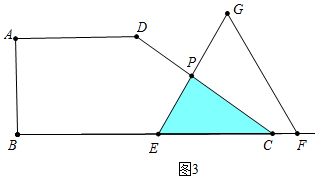
y=$\frac{\sqrt{3}}{8}$��6-x��2=$\frac{\sqrt{3}}{8}$x2-$\frac{3\sqrt{3}}{3}$x+$\frac{9\sqrt{3}}{2}$��
���� ���⿼���ı����ۺ��⡢�ȱ������ε����ʡ�������Ǻ��������������ε��ж������ʡ�����ε������֪ʶ������Ĺؼ���ѧ���÷������۵�˼��˼�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 628ml | B�� | 603ml | C�� | 588ml | D�� | 568ml |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
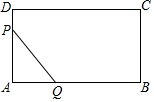 ��֪����ABCD��AB=10��BC=5����P��2��λ/����ٶȴ�A������AD-DC-CB����B����Q��1��λ/����ٶȴ�A������AB����B����P��Qͬʱ��������APQ�����y���˶�ʱ��x��ı仯�Ĵ���ͼ���ǣ�������
��֪����ABCD��AB=10��BC=5����P��2��λ/����ٶȴ�A������AD-DC-CB����B����Q��1��λ/����ٶȴ�A������AB����B����P��Qͬʱ��������APQ�����y���˶�ʱ��x��ı仯�Ĵ���ͼ���ǣ�������| A�� | 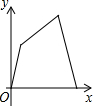 | B�� | 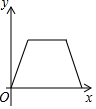 | C�� | 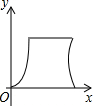 | D�� | 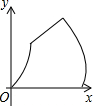 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x•��-xy��2=-2x3y | B�� | ��-x2��3�£�-x3��2=1 | ||
| C�� | ��$\frac{3}{4}$a3-$\frac{1}{2}$b��•2ab=$\frac{3}{2}$a4b-ab2 | D�� | ��3m-1��2=9m2-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
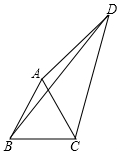 ��ͼ���ı���ABCD�У�AC��BD�ǶԽ��ߣ���ABC�ǵȱ������Σ���ADC=30�㣬AD=3��BD=5��
��ͼ���ı���ABCD�У�AC��BD�ǶԽ��ߣ���ABC�ǵȱ������Σ���ADC=30�㣬AD=3��BD=5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
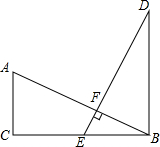 ��ͼ����֪AC��CB��DB��CB��AB��DE��AB=DE��E��BC���е㣮
��ͼ����֪AC��CB��DB��CB��AB��DE��AB=DE��E��BC���е㣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com