
【题目】计算:
(1)(﹣3y)(4x﹣3x2﹣1);
(2)(2x+3)(x﹣7);
(3)(-1)2019+(3-π)0 +2-2+ 4101×0.25100;
(4)2019220182020.(运用乘法公式计算)
科目:初中数学 来源: 题型:
【题目】将正面分别标有数字1、2、3的三张卡片洗匀后,背面朝上放在桌面上请完成下列各题
(1)随机抽取1张,求抽到卡片数字是奇数的概率;
(2)随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成哪些两位数?
(3)在(2)的条件下,试求组成的两位数是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
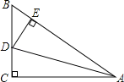
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论.①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB,其中正确的是____________
查看答案和解析>>
科目:初中数学 来源: 题型:
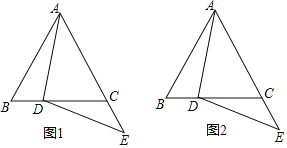
【题目】在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)点E关于直线BC的对称点为M,连接DM,AM.
①依题意将图2补全;
②小姚通过观察、实验提出猜想:在点D运动的过程中,始终有DA=AM,小姚把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明DA=AM,只需证△ADM是等边三角形;
想法2:连接CM,只需证明△ABD≌△ACM即可.
请你参考上面的想法,帮助小姚证明DA=AM(一种方法即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在给定的一张平行四边形纸片上按如下操作:连结AC,作AC的垂直平分线MN分别交AD、AC、BC于M、O、N,连结AN,CM,则四边形ANCM是( )

A. 矩形 B. 菱形 C. 正方形 D. 无法判断
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD 和折线 OABC 表示“龟兔赛跑”时的路程与时间关系,请你根据图中给出的信息,解决下列问题:
(1)折线 OABC 表示赛跑过程中_______的路程与时间的关系, 线段 OD 表示赛跑过程中_______的路程与时间的关系, 赛跑的全程是________米.
(2)兔子在起初每分钟跑多少米,乌龟用多少分钟追上了正在睡觉的兔子.
(3)兔子醒来,以 48 千米/小时的速度跑向终点,结果还是比乌龟晚到 0.5 分钟,请你算算兔子中间停下睡觉用了多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
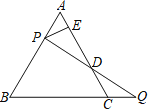
【题目】如图,过边长为2的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连接PQ交AC边于D,则DE的长为( )
A.![]() B.1C.
B.1C.![]() D.不能确定
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收33万元.而该游乐设施开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数;
(1)若维修保养费用第1个月为2万元,第2个月为4万元.求y关于x的解析式;
(2)求纯收益g关于x的解析式;
(3)问设施开放几个月后,游乐场的纯收益达到最大;几个月后,能收回投资?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com