
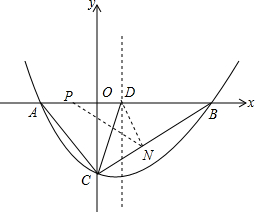
 已知抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,-8),对称轴为x=4.
已知抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,-8),对称轴为x=4.分析 (1)由题意抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,-8),对称轴为x=4,根据待定系数法可以求得该抛物线的解析式;
(2)假设存在,设出时间t,则根据线段PN被直线CD垂直平分,再由垂直平分线的性质及勾股定理来求解t,看t是否存在;
(3)假设直线x=1上是存在点M,使△MPN为等腰三角形,此时要分两种情况讨论:①当PN为等腰△MPN的腰时,且P为顶点;②当PN为等腰△MPN的腰时,且Q为顶点;然后再根据等腰三角形的性质及直角三角形的勾股定理求出M点坐标.
解答 解:(1)∵抛物线过C(0,-8),
∴c=-8,即y=ax2+bx-8,
由函数经过点(14,0)及对称轴为x=4可得$\left\{\begin{array}{l}{-\frac{b}{2a}=4}\\{196a+14b-8=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{2}{21}}\\{b=-\frac{16}{21}}\end{array}\right.$,
∴该抛物线的解析式为y=$\frac{2}{21}$x2-$\frac{16}{21}$x-8. (2)存在直线CD垂直平分PN.
(2)存在直线CD垂直平分PN.
由函数解析式为y=$\frac{2}{21}$x2-$\frac{16}{21}$x-8,可求出点A坐标为(-6,0),
在Rt△AOC中,AC=$\sqrt{A{O}^{2}+O{C}^{2}}$=$\sqrt{100}$=10=AD,
故可得OD=AD-OA=4,点D在函数的对称轴上,
∵线CD垂直平分PN,
∴∠PDC=∠NDC,PD=DN,
由AD=AC可得,∠PDC=∠ACD,
∴∠NDC=∠ACD,
∴DN∥AC,
又∵DB=AB-AD=20-10=10=AD,
∴点D是AB中点,
∴DN为△ABC的中位线,
∴DN=$\frac{1}{2}$AC=5,
∴AP=AD-PD=AD-DN=10-5=5,
∴t=5÷1=5(秒),
∴存在t=5(秒)时,线段PN被直线CD垂直平分.
在Rt△BOC中,BC=$\sqrt{O{C}^{2}+O{B}^{2}}$=$\sqrt{{8}^{2}+1{4}^{2}}$=2$\sqrt{65}$,
而DN为△ABC的中位线,N是BC中点,
∴CN=$\sqrt{65}$,
∴点N的运动速度为每秒$\frac{\sqrt{65}}{5}$单位长度;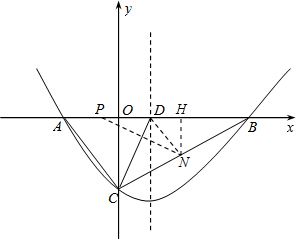 (3)存在,过点N作NH⊥x轴于H,则NH=$\frac{1}{2}$OC=4,PH=OP+OH=1+7=8,
(3)存在,过点N作NH⊥x轴于H,则NH=$\frac{1}{2}$OC=4,PH=OP+OH=1+7=8,
在Rt△PNH中,PN=$\sqrt{{4}^{2}+{8}^{2}}$=$\sqrt{80}$=4$\sqrt{5}$,
①当MP=MN,即M为顶点,则此时CD与PN的交点即是M点(上面已经证明CD垂直平分PN),
设直线CD的直线方程为:y=kx+b(k≠0),
因为点C(0,-8),点D(4,0),
所以可得直线CD的解析式为:y=2x-8,
当x=1时,y=-6,
∴M1(1,-6);
②当PN为等腰△MPN的腰时,且P为顶点.
设直线x=1上存在点M(1,y),因为点P坐标为(-1,0),
从而可得PM2=22+y2,
又PN2=80,
则22+y2=80,
即y=±2$\sqrt{19}$,
∴M2(1,2$\sqrt{19}$),M3(1,-2$\sqrt{19}$);
③当PN为等腰△MPN的腰时,且N为顶点,点N坐标为(7,-4),
设直线x=1存在点M(1,y),
则NM2=62+(y+4)2=80,
解得:y=2$\sqrt{11}$-4或-2$\sqrt{11}$-4;
∴M4(1,-4+2$\sqrt{11}$),M5(1,-4-2$\sqrt{11}$).
综上所述:存在这样的五点:M1(1,-6),M2(1,2$\sqrt{19}$),M3(1,-2$\sqrt{19}$),M4(1,-4+2$\sqrt{11}$),M5(1,-4-2$\sqrt{11}$).
点评 此题是一道综合题,难度较大,主要考查二次函数的性质,用待定系数法求函数的解析式,还考查等腰三角形的性质,同时还让学生探究存在性问题,对待问题要思考全面,学会分类讨论的思想.


科目:初中数学 来源: 题型:选择题
| A. | A+B是关于x的5次多项式 | B. | A-B是关于x的4次多项式 | ||
| C. | AB是关于x的10次多项式 | D. | $\frac{A}{B}$是与x无关的常数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
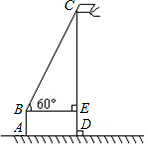 小明周日在广场放风筝,如图,小明为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为20米,小明的身高AB为1.75米,请你帮小明计算出风筝离地面的高度.(结果精确到0.1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
小明周日在广场放风筝,如图,小明为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为20米,小明的身高AB为1.75米,请你帮小明计算出风筝离地面的高度.(结果精确到0.1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
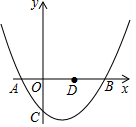 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c(b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,且OB=2OC.
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c(b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,且OB=2OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
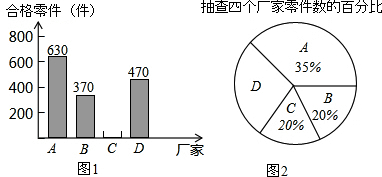
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
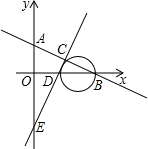 已知直线y=-$\frac{1}{2}$x+1与x轴、y轴分别交于B点、A点,直线y=2x-2与x轴、y轴分别交于D点、E点,两条直线交于点C;
已知直线y=-$\frac{1}{2}$x+1与x轴、y轴分别交于B点、A点,直线y=2x-2与x轴、y轴分别交于D点、E点,两条直线交于点C;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
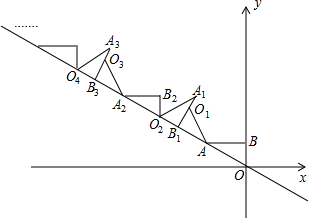 如图,AB⊥y轴,垂足为B,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=-$\frac{\sqrt{3}}{3}$x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=-$\frac{\sqrt{3}}{3}$x上,依次进行下去…若点B的坐标是(0,1),则点O12的纵坐标为9+3$\sqrt{3}$.
如图,AB⊥y轴,垂足为B,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=-$\frac{\sqrt{3}}{3}$x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=-$\frac{\sqrt{3}}{3}$x上,依次进行下去…若点B的坐标是(0,1),则点O12的纵坐标为9+3$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com