
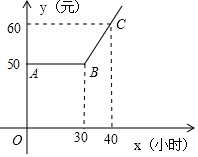
 某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.分析 (1)设函数解析式为y=kx+b,把B、C两点坐标代入列出方程组,解方程组即可;
(2)根据函数图象,可知上网20小时的费用;
(3)求y=98时x的值即可;
解答 解:(1)当x≥30时,设y与x之间的函数关系式为y=kx+b,
由题意$\left\{\begin{array}{l}{30k+b=50}\\{40k+b=60}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=20}\end{array}\right.$,
∴y=x+20.
(2)若小王4月份上网20小时,由图象可知,他应付50元的上网费.
(3)把y=98代入,y=x+20,解得x=78,
∴若小王5月份上网费用为98元,则他在该月份的上网时间是78小时.
点评 此题考查一次函数的应用,待定系数法等知识,解题的关键是熟练掌握待定系数法确定函数解析式,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
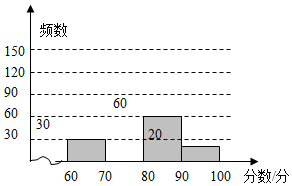 为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:
为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | m | 0.45 |
| 80≤x<90 | 60 | n |
| 90≤x≤100 | 20 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
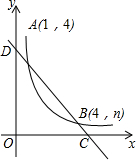 如图,直线y1=ax+b与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于A(1,4)、B(4,n)两点,与x轴、y轴交于C、D两点.
如图,直线y1=ax+b与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于A(1,4)、B(4,n)两点,与x轴、y轴交于C、D两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
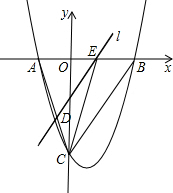 如图,抛物线y=$\frac{4}{3}$x2-$\frac{8}{3}$x-4与x轴交于A,B两点,与y轴交于点C,连接BC,AC.
如图,抛物线y=$\frac{4}{3}$x2-$\frac{8}{3}$x-4与x轴交于A,B两点,与y轴交于点C,连接BC,AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com