
 已知:如图,△ABC是⊙O内接三角形,OM⊥AB于点M,ON⊥AC于点N,连接MN,
已知:如图,△ABC是⊙O内接三角形,OM⊥AB于点M,ON⊥AC于点N,连接MN,分析 (1)由垂径定理和三角形的中位线的性质得到结论.
(2)由AD是⊙O的直径,得到∠ABD=90°,解直角三角形得到AD,AB的长度,再由锐角三角函数解出结果.
解答 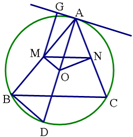 (1)证明:∵OM⊥AB于点M,ON⊥AC于点N,
(1)证明:∵OM⊥AB于点M,ON⊥AC于点N,
∴点M、N分别是AB、AC的中点,MN是三角形ABC的中位线,
∴MN=$\frac{1}{2}$BC;
(2)解:∵AD是⊙O的直径,
∴∠ABD=90°,
∵cos∠BAD=$\frac{4}{5}$,BD=20,
∴在直角三角形ABD中,可设AD=5k,AB=4K,
根据勾股定理得:(5k)2-(4k)2202,
∴k=$±\frac{20}{3}$(-$\frac{20}{3}$舍去),
∴AD=$\frac{100}{3}$,AB=$\frac{80}{3}$,
∵AG是⊙O的切线,
∴OA⊥AG,
又∵MG⊥AG,
∴∠GAD=90°=∠MGA,
∴AD∥MG
∴∠AMG=∠BAD
∴sin∠AMG=sin∠BAD=$\frac{AG}{AM}$=$\frac{BD}{AD}$=$\frac{3}{5}$,
∴AG=$\frac{3}{5}$AM=$\frac{3}{5}$×$\frac{1}{2}$AB=8,
∴AG=8.
点评 本题考查了三角形的中位线定理,切线的性质,垂径定理,勾股定理,锐角三角函数,掌握垂径定理是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
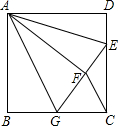 如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①点G是BC中点;②FG=FC;③S△FGC=$\frac{9}{10}$.其中正确的有①③(填写序号).
如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①点G是BC中点;②FG=FC;③S△FGC=$\frac{9}{10}$.其中正确的有①③(填写序号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AE•AD=AH•AF;其中结论正确的个数是( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AE•AD=AH•AF;其中结论正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届福建省仙游县郊尾、枫亭五校教研小片区九年级下学期第一次月考数学试卷(解析版) 题型:填空题
某商场进行平板电脑促销活动,降价15%后,又降低了150元,此时售价为2400元,则该平板电脑原价为________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com