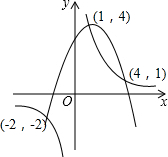练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．二次函数y=ax2+bx+c（a≠0）的图象与反比例函数y=$\frac{k}{x}$（k≠0）的图象相交（如图），则不等式ax2+bx+c＞$\frac{k}{x}$的解集是（　　）
    A．1＜x＜4或x＜-2B．1＜x＜4或-2＜x＜0
    C．0＜x＜1或x＞4或-2＜x＜0D．-2＜x＜1或x＞-4

    分析 根据图象的上下位置直接写出不等式ax2+bx+c＞$\frac{k}{x}$的解集．

    解答 解：由图象可知，抛物线在双曲线上面的就是不等式ax2+bx+c＞$\frac{k}{x}$的解集，
    即：-2＜x＜0或1＜x＜4，
    故选B，

    点评 此题是二次函数和不等式题，主要考查二次函数的图象和双曲线的图象，解本题的关键是识别函数图象．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    20．下列调查中，调查方式不合理的是（　　）
    A．用抽样调查了解广州市中学生每周使用手机所用的时间
    B．用全面调查了解某班学生对6月5日是“世界环境日”的知晓情况
    C．用抽样调查选出某校短跑最快的学生参加全市比赛
    D．用抽样调查了解南沙区初中学生零花钱的情况

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．正方形的面积是4cm2，那么对角线是（　　）cm．
    A．2cmB．4cmC．2$\sqrt{2}$ cmD．$\sqrt{2}$ cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．已知：平行四边形的两条对角线长分别为10和14，则此平行四边形边长x的取值范围是2＜x＜12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图CO是等腰△ABC底边AB上的高，AB=6，点P从点C出后沿CO以ka个单位/秒的速度到达点G，再沿GA以a个单位/秒的速度到达点A．
    （1）当CO=3$\sqrt{3}$，CG=2$\sqrt{3}$时，点P的运动距离=4$\sqrt{3}$．
    （2）当CO=3$\sqrt{3}$且满足k=2，a=1时，求运动时间t的最小值．
    （3）当CO=6，其余条件不变时，取K=$\sqrt{5}$时，存在最短运动时间，此时OG的长=$\frac{3}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．定义：如图1，点M、N把线段AB分割成AM、MN、NB，若以AM、MN、NB为边的三角形是一个直角三角形，则称点M、N是线段AB的勾股分割点．
    （1）已知M、N把线段AB分割成AM、MN、NB，若AM=2，MN=4，BN=2$\sqrt{3}$，则点M、N是线段AB的勾股分割点；（填“是”或“不是”）
    （2）已知点M、N是线段AB的勾股分割点，若AB=12，AM=5，求BN的长；
    （3）如图2，P、Q是等腰Rt△ABC斜边AB的勾股分割点，PQ＞AP，PQ＞BQ，求∠PCQ的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，扇形OAB的圆心角∠AOB=120°，半径OA=6cm．
    （1）请你用尺规作图的方法作出扇形的对称轴（不写作法，保留作图痕迹）；
    （2）求弧AB的长及扇形OAB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．计算（-3）2003÷（-3）2005的结果为（　　）
    A．9B．-9C．$\frac{1}{9\;}$D．$-\frac{1}{9\;}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，在Rt△ABC中，∠ACB=90°，AB=5，AC=3，过点C作直线MN∥AB，点P为直线MN上的一动点（不与C点重合），∠PAB的平分线交BC于E． 设CP=x，AP=y．
    （1）若PA与线段BC交于点D，且CP=1，求CD的长；
    （2）若△ABE为等腰三角形，求y关于x的函数关系式；
    （3）若PA与线段BC交于点D，△AEP是直角三角形，求CP的长．

    查看答案和解析>>

    同步练习册答案