分析:(1)先去分母,然后移项、合并同类项;
(2)分别解答不等式组中的两个不等式的解集,然后求其交集即为不等式组的解集;
然后把它们的解集在数轴上表示出来.
解答:解:(1)由原不等式,得
3x+3-2x≥5,
即x+3≥5,
不等式的两边同时减去3,得
x≥2(如图所示);

(2)
解①得,x>
,
解②得,x≤4,
∴原不等式组的解集是:
<x≤4(如图所示):
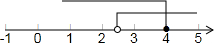
点评:本题主要考查了一元一次不等式(组)解集的求法、在数轴上表示不等式的解集.把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.





 初中学业考试导与练系列答案
初中学业考试导与练系列答案