
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B,C重合),经过点O、P折叠该纸片,得点B′和折痕OP(如图①)经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ(如图②),当点C′恰好落在OA上时,点P的坐标是 . 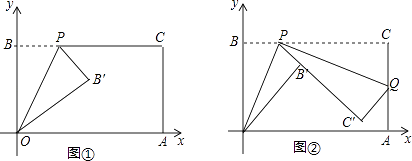
【答案】![]() 或
或 ![]()
【解析】解: 
∵把△OPB沿OP折叠,使点C落在点C′处,
∴BP=PB′,OB=OB′=6,∠A=∠OB′P=90°,
∵把△CPQ沿PQ折叠,使点D落在直线OA上的点C′处,
∴CP=C′P,CQ=C′Q,∠PC′Q=∠C=90°,
设BP=B′P=x,则PC=PC′=11﹣x,
∵BC∥AC,
∴∠1=∠EPOA,
∵∠1=∠2,
∴∠2=∠C′OP,
∴OC′=PC′=11﹣x,
∴B′C′=11﹣2x,
在Rt△OB′C′中,
∵OC′2=OB′2+B′C′2 ,
∴62+(11﹣2x)2=(11﹣x)2 ,
解得x= ![]() ,
,
∴AE= ![]() 或
或 ![]() .
.
故答案为 ![]() 或
或 ![]() .
.
设PB=B′P=x,则DE=ED′=15﹣x,只要证明PC=PC′=11﹣x,在Rt△OB′C′中,根据OC′2=OB′2+B′C′2 , 列出方程即可解决问题.


科目:初中数学 来源: 题型:
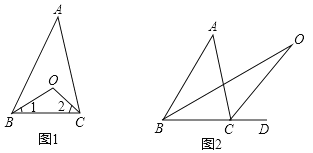
【题目】认真阅读下面关于三角形内外角平分线的研究片断,完成所提出的问题.
探究1:如图(1)在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+![]() ∠A,理由如下:
∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线,∴∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACB.
∠ACB.
∴∠1+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A.
∠A.
∴∠BOC=180°-(∠1+∠2)=180°-(90°-![]() ∠A)=90°+
∠A)=90°+![]() ∠A
∠A
探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b经过点A(0,6),且平行于直线y=-2x.
(1)求该函数的解析式,并画出它的图象;
(2)如果这条直线经过点P(m,2),求m的值;
(3)若O为坐标原点,求直线OP的解析式;
(4)求直线y=kx+b和直线OP与坐标轴所围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保证学生有足够的睡眠,政协委员于今年两会向大会提出一个议案,即“推迟中小学生早晨上课时间”,这个议案当即得到不少人大代表的支持.根据北京市教委的要求,学生小强所在学校将学生到校时间推迟半小时.小强原来7点从家出发乘坐公共汽车,7点20分到校;现在小强若由父母开车送其上学,7点45分出发,7点50分就到学校了.已知小强乘自家车比乘公交车平均每小时快36千米,求从小强家到学校的路程是多少千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解同学对体育活动的喜爱情况,某校设计了“你最喜欢的体育活动是哪一项(仅限一项)”的调查问卷.该校对本校学生进行随机抽样调查,以下是根据调查数据得到的统计图的一部分.请根据以上信息解答以下问题:
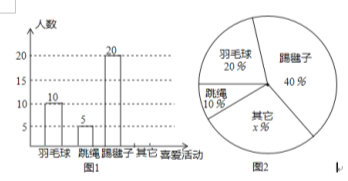
(1)该校对多少名学生进行了抽样调查?
(2)①请补全图1并标上数据 ②图2中x= .
(3)若该校共有学生900人,请你估计该校最喜欢跳绳项目的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱我中华”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:甲:8,7,9,8,8;乙:7,9,6,9,9,则下列说法中错误的是( )
A. 甲、乙得分的平均数都是8 B. 甲得分的众数是8,乙得分的众数是9
C. 甲得分的中位数是9,乙得分的中位数是6 D. 甲得分的方差比乙得分的方差小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于点A(﹣1,0)、B(3,0)、点C三点.
(1)试求抛物线的解析式;
(2)点D(2,m)在第一象限的抛物线上,连接BC、BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由;
(3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′.在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒,试求S与t之间的函数关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点G在对角线BD上![]() 不与点
不与点![]() 重合
重合![]() 于点
于点![]() 于点F,连结AG.
于点F,连结AG.
![]() 写出线段
写出线段![]() 长度之间的数量关系,并说明理由;
长度之间的数量关系,并说明理由;
![]() 若正方形ABCD的边长为
若正方形ABCD的边长为![]() ,求线段BG的长.
,求线段BG的长.
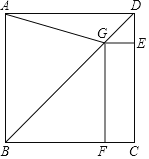
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P作BC的平行线,分别交AC于点F、Q,记△AEF的面积为S1 , 四边形EFQP的面积为S2 , 四边形PQCB的面积为S3 . 
(1)求证:EF+PQ=BC;
(2)若S1+S3=S2 , 求![]() 的值;
的值;
(3)若S3﹣S1=S2 , 直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com