
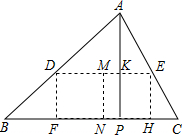
 如图,△ABC是一块锐角三角形余料,边长BC=120cm,高AP=90cm,现在要把它加工成长方形零件DFHE,且满足FH=2DF,F、H在BC上,D、E分别在AB、AC上,求短边DF的长.
如图,△ABC是一块锐角三角形余料,边长BC=120cm,高AP=90cm,现在要把它加工成长方形零件DFHE,且满足FH=2DF,F、H在BC上,D、E分别在AB、AC上,求短边DF的长.  轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:解答题
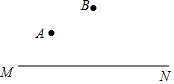 A、B两厂在公路MN同侧,拟在公路边建一货场C,若由B厂独家兴建,并考虑B厂的利益,则要求货场离B厂最近,请在图中作出此时货场C的位置,并说出这样做的道理.
A、B两厂在公路MN同侧,拟在公路边建一货场C,若由B厂独家兴建,并考虑B厂的利益,则要求货场离B厂最近,请在图中作出此时货场C的位置,并说出这样做的道理.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 1-$\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐标系中的图象,可能是( )
二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐标系中的图象,可能是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
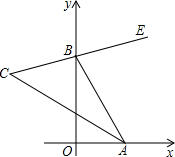 如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明.
如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知等腰直角三角ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b
如图,已知等腰直角三角ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com