
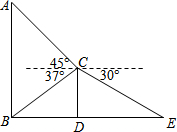
 某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为9米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.
某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为9米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.分析 (1)由在Rt△CDE中,tan∠CED=$\frac{DC}{DE}$,DE=9,∠CED=30°,即可求得答案;
(2)首先过点C作CF⊥AB于点F,然后在Rt△CBF中,求得FC,在Rt△AFC中,求得AF,继而求得答案.
解答  解:(1)在Rt△CDE中,tan∠CED=$\frac{DC}{DE}$,DE=9,∠CED=30°,
解:(1)在Rt△CDE中,tan∠CED=$\frac{DC}{DE}$,DE=9,∠CED=30°,
∴tan30°=$\frac{DC}{9}$,
解得:DC≈$\frac{9}{1.73}$≈5.2,
∴建筑物CD的高度约为5.2米;
(2)过点C作CF⊥AB于点F.
在Rt△CBF中,tan∠FCB=$\frac{BF}{FC}$,BF=DC=5.2,∠FCB=37°,
∴tan37°=$\frac{5.2}{FC}$≈$\frac{3}{4}$,FC≈6.93,
在Rt△AFC中,∵∠ACF=45°,
∴AF=CF=6.93,
∴AB=AF+BF≈12.13,
∴建筑物AB的高度约为12.13米.
点评 此题考查了俯角与仰角的定义.注意能借助俯角与仰角构造直角三角形并解直角三角形是解此题的关键.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:选择题
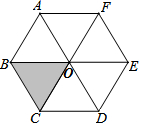 如图,六边形ABCDEF是由6个相同的等边三角形组成的,在这些三角形中,可以由△OBC平移得到的有( )个三角形.
如图,六边形ABCDEF是由6个相同的等边三角形组成的,在这些三角形中,可以由△OBC平移得到的有( )个三角形.| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
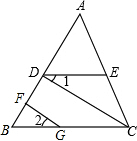 已知:如图,CD⊥AB,GF⊥AB,∠B=∠ADE.
已知:如图,CD⊥AB,GF⊥AB,∠B=∠ADE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7×10-6cm | B. | 0.7×108cm | C. | 0.7×10-8cm | D. | 7×10-7cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
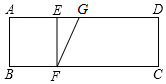 如图,在矩形ABCD中,AB=2,AD=6,E.F分别是线段AD,BC上的点,连接EF,使四边形ABFE为正方形,若点G是AD上的动点,连接FG,将矩形沿FG折叠使得点C落在正方形ABFE的对角线所在的直线上,对应点为P,则线段AP的长为4或4-2$\sqrt{2}$.
如图,在矩形ABCD中,AB=2,AD=6,E.F分别是线段AD,BC上的点,连接EF,使四边形ABFE为正方形,若点G是AD上的动点,连接FG,将矩形沿FG折叠使得点C落在正方形ABFE的对角线所在的直线上,对应点为P,则线段AP的长为4或4-2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
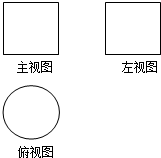 如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )
如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )| A. | $\frac{π}{4}$ | B. | $\frac{5π}{4}$ | C. | π | D. | $\frac{3π}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com