练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，已知O为原点，点A的坐标为(4，3)，⊙A的半径为2．过A作直线l平行于x轴，点P在直线l上运动．当点P的横坐标为12时，直线OP与⊙A的位置关系是________．

    答案：相交
    解析：

    如图所示，作AC⊥OP，点C为垂足．

    ∵∠ACP=∠OBP=90°，∠1=∠1，

    ∴△ACP∽△OBP，∴．

    在Rt△OBP中，．

    又AP=12－4=8，∴，

    ∴，

    ∴OP与⊙A相交．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

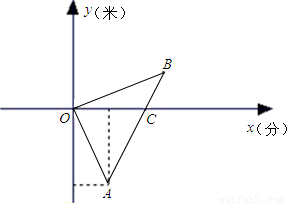
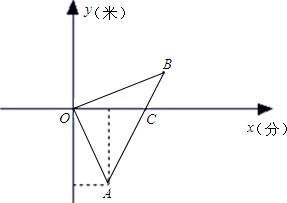    早晨小欣与妈妈同时从家里出发，步行与骑自行车到方向相反的两地上学与上班．妈妈骑车走了一会接到小欣的电话，即以原速骑车前往小欣学校，并与小欣同时到达学校．他们离家的路程y （米）与时精英家教网间x （分）的函数图象如图所示．已知A点坐标A（10，-2500），C（20，0）C点坐标为（20，0）．
    （1）在图中，小明离家的路程y （米）与时间x （分）的函数图象是线段；
    A、OA     B、OB      C、OC      D、AB
    （2）分别求出线段OA与AB的函数表达式（不需要写出自变量的取值范围）；
    （3）已知小欣步行速度为每分50米，则小欣家与学校距离为多少米，小欣早晨上学需要多少分钟？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

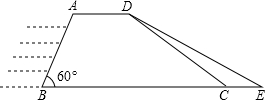    水务部门为加强防汛工作，决定对程家山水库进行加固．原大坝的横断面是梯形ABCD，如图所示，已知迎水面AB的长为10米，∠B=60°，背水面精英家教网DC的长度为10
    		3
    米，加固后大坝的横断面为梯形ABED．若CE的长为5米．
    （1）已知需加固的大坝长为100米，求需要填方多少立方米；
    （2）求新大坝背水面DE的坡度．（计算结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

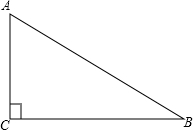    精英家教网如图所示，已知：Rt△ABC中，∠ACB=90°．
    （1）尺规作图：作∠BAC的平分线AM交BC于点D（只保留作图痕迹，不写作法）；
    （2）在（1）所作图形中，将Rt△ABC沿某条直线折叠，使点A与点D重合，折痕EF交AC于点E，交AB于点F，连接DE、DF，再展回到原图形，得到四边形AEDF．
    ①试说明四边形AEDF为平行四边形；
    ②若AB=10，BC=8，在折痕EF上有一动点P，求PC+PD的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

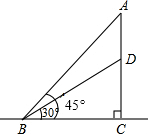    在合肥市地铁一号线的修建过程中，原设计的地铁车站出入口高度较低，为适应地形，把地铁车站出入口上下楼梯的高度普遍增加了，如图所示，已知原设计楼梯BD长20米，在楼梯水平长度（BC）不发生改变的前提下，楼梯的倾斜角由30°增大到45°，那么新设计的楼梯高度将会增加多少米？（结果保留整数，参考数据：
    		2
    ≈1.414，
    		3
    ≈1.732）

    查看答案和解析>>

    科目：初中数学 来源：2010年江苏省南京市浦口区中考数学二模试卷（解析版） 题型：解答题

    （2010•鼓楼区二模）早晨小欣与妈妈同时从家里出发，步行与骑自行车到方向相反的两地上学与上班．妈妈骑车走了一会接到小欣的电话，即以原速骑车前往小欣学校，并与小欣同时到达学校．他们离家的路程y （米）与时间x （分）的函数图象如图所示．已知A点坐标A（10，-2500），C（20，0）C点坐标为（20，0）．
    （1）在图中，小明离家的路程y （米）与时间x （分）的函数图象是线段；
    A、OA     B、OB      C、OC      D、AB
    （2）分别求出线段OA与AB的函数表达式（不需要写出自变量的取值范围）；
    （3）已知小欣步行速度为每分50米，则小欣家与学校距离为多少米，小欣早晨上学需要多少分钟？

    查看答案和解析>>

    同步练习册答案