
【题目】如图,四边形ABCD中,∠A = ∠B = 90°,AB边上有一点E,CE,DE分别是∠BCD和∠ADC 的角平分线,如果ABCD的面积是12,CD = 8,那么AB的长度为_____.

【答案】3
【解析】
根据角平分线的定义求出∠ADE=∠CDE,∠DCE=BCE,求出∠DCE+∠CDE=90°,延长DE交CB的延长线于点F,求出△CDF是等腰三角形;求出DE=FE,根据全等三角形的判定得出△BEF≌△AED,得到AD=BF,故FC=AD+BC=CD,再根据等腰梯形的面积公式即可求解AB的长.
∵∠A = ∠B = 90°
∴AD∥BC,∠ADC+∠BCD=180
∵ED平分∠ADC,EC平分∠BCD,
∴∠ADE=∠CDE,∠DCE=BCE
∴∠DCE+∠CDE=90
∴DE⊥EC,
延长DE交CB的延长线于点F,
∵AD∥BC,DE是∠ADC的角平分线,
∴∠CDF=∠ADE=∠DFC,
∴CD=CF,
∴△CDF是等腰三角形;
∵DE⊥EC,
∴DE=FE,
在△BEF和△AED中
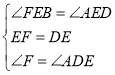
∴△BEF≌△AED(ASA),
∴AD=BF,
故FC=AD+BC=CD=8,
∵等腰梯形的面积为![]() (AD+BC)×AB=12
(AD+BC)×AB=12
即![]() ×8×AB=12
×8×AB=12
故AB=3.
故填:3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】请认真阅读下面的数学小探究系列,完成所提出的问题:
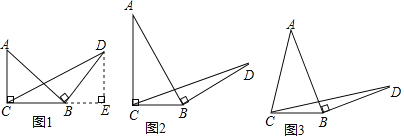
![]() 探究1:如图1,在等腰直角三角形ABC中,
探究1:如图1,在等腰直角三角形ABC中,![]() ,
,![]() ,将边AB绕点B顺时针旋转
,将边AB绕点B顺时针旋转![]() 得到线段BD,连接
得到线段BD,连接![]() 求证:
求证:![]() 的面积为
的面积为![]() 提示:过点D作BC边上的高DE,可证
提示:过点D作BC边上的高DE,可证![]() ≌
≌![]()
![]() 探究2:如图2,在一般的
探究2:如图2,在一般的![]() 中,
中,![]() ,
,![]() ,将边AB绕点B顺时针旋转
,将边AB绕点B顺时针旋转![]() 得到线段BD,连接
得到线段BD,连接![]() 请用含a的式子表示
请用含a的式子表示![]() 的面积,并说明理由.
的面积,并说明理由.
![]() 探究3:如图3,在等腰三角形ABC中,
探究3:如图3,在等腰三角形ABC中,![]() ,
,![]() ,将边AB绕点B顺时针旋转
,将边AB绕点B顺时针旋转![]() 得到线段BD,连接
得到线段BD,连接![]() 试探究用含a的式子表示
试探究用含a的式子表示![]() 的面积,要有探究过程.
的面积,要有探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
(1)B出发时与A相距 千米。
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是 小时。
(3)B出发后 小时与A相遇。
(4)求出A行走的路程S与时间t的函数关系式。
(5)求出当 t≥1.5时B走的路程S与时间t的函数关系式

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中能判断△ABC为直角三角形的是( )
A.∠A +∠B = ∠CB.∠A = ∠B = ∠C
C.∠A-∠B = 90°D.∠A = ∠B = 3∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下关于x的各个多项式中,a,b,c,m,n均为常数.
(1)根据计算结果填写下表:
二次项系数 | 一次项系数 | 常数项 | |
(2x + l)(x + 2) | 2 | 2 | |
(2x + 1)(3x - 2) | 6 | -2 | |
(ax + b)( mx + n) | am | bn |
(2)已知(x+ 3)2(x + mx +n)既不含二次项,也不含一次项,求m + n的值.
(3) 多项式M与多项式x2-3x + 1的乘积为2x4+ ax3 + bx2+ cx -3,则2 a +b + c的值为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB垂直平分线段CD(AB>CD),点E是线段CD延长线上的一点,且BE=AB,连接AC,过点D作DG⊥AC于点G,交AE的延长线与点F.
(1)若∠CAB=α,则∠AFG= (用α的代数式表示);
(2)线段AC与线段DF相等吗?为什么?
(3)若CD=6,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=5,AC=4,∠B,∠C的平分线相交于点O,OM∥AB,ON∥AC分别与BC交于点M、N,则△OMN的周长为____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com